Externalities and Public Good (With Diagram)

Let us make an in-depth study of the externalities and public good.

Externality:

An externality exists if some of the variables which affect one decision-maker’s utility or profit are under the control of another decision-maker.

For example, a chemical works which pumps effluent into the stream will affect the cost of producing beer in a brewery industry downstream because of its choice of output level and input combinations and the amount of effluent which needs to be removed from the water before it can be used in beer production.

In this case, the externality is detrimental, but in other cases, there may be beneficial externalities, as for example, when an apple-grower is located next to a bee-keeper. The bees will cross-pollinate the apple trees, benefiting the apple- grower, and feed off the apple blossom, benefiting the bee-keeper as well.

This is an example of reciprocal externality. In addition, there may be consumer externalities, producer-consumer externalities and consumer-producer externalities.

Let us see why externalities may lead to inefficiency. We consider again the example of the upstream chemical factory and the downstream brewery. The chemical factory will fix its output level to maximise its profits and will not take into consideration the effects of its pollution on the profits of the brewery industry.

But the brewery would be willing to pay the chemical factory to reduce the amount of effluent, because, this will reduce the costs of brewery industry.

Such a reduction in effluent may reduce the chemical industry’s profits, as the firm’s output of chemicals and the effluents are in fixed proportions and any reduction of effluent, thus, requires a reduction in output of the chemical industry.

If the reduction in the brewery industry’s costs exceeds the reduction in the chemical factory’s profit, there are potential gains from trade and the original level of effluent cannot have been efficient. This observation leads to a possible solution to the externality problem presented by Coase.

Coase Theorem:

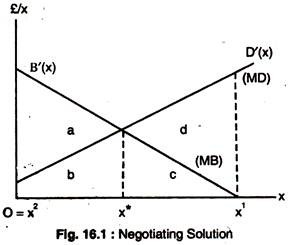
Assuming that the chemical factory produces its output and the effluent in fixed proportions, we can write its profit as a function of effluent, which is x, as: B(x). The damage produced by the chemical factory downstream due to pollution is D(x). Fig. 16.1 shows the marginal benefit (MB) B ‘(x) and marginal damage (MD) D’ (x) from polluting downstream.

Assume that the profits of the two firms measure the social value of their outputs and that the effluent does not impose costs on any other individuals or firms, then the efficient level of pollution which maximises the profits of the two firms is given by x* which satisfies : B'(x*) – D'(x*) = 0………… (1)

Consider two possible legal situations, which will be determined by which firm sets up business first:

(a) Permissive:

Suppose the chemical firm has the legal right to discharge as much effluent as it wishes. Thus, it controls effluent, x, and would choose a level x¹, where B'(x) = 0. Here the level of pollution is inefficiently large as its effect on the brewery ‘ firm is ignored.

(b) Restrictive:

The chemical firm has no legal right to discharge effluent and the brewery firm can obtain a court order to prevent it from doing so. In such a situation, it is the brewery firm which controls the level of pollution and chooses a level of x² – 0, where its costs from the effluent are minimised. A zero level of pollution is also inefficient since the brewery firm ignores the effect of its choice on the profit of the chemical firm.

Since x² and x¹ are inefficient, there are potential gains from trade, i.e., from a contract between the two firms to control the pollution level. Suppose the legal action considers a reduction of pollution to x* from x¹. The reduction in the chemical firm’s profit is c and the reduction in the brewery firm’s costs is c + d.

A payment by the brewery firm to the chemical firm of c + dQ (0 < Q < 1) in exchange for a reduction in pollution from x¹ to x* would achieve an efficient allocation of resources and make both firms better-off. The contract would generate a combined gain from trade of d.

If the legal regime is restrictive, a contract in which the chemical firm paid the brewery Qa + b, in exchange for an increase in effluent from zero to x* would lead to an efficient level of pollution and make both parties better-off.

The payment to the brewery would more than compensate for the increase in costs b and the chemical firm’s profit would increase by a + b which would more than cover the payment to the brewery. The contract would split the gains from trade between the two firms.

This result is known as Coase Theorem: “Bargaining can achieve an efficient allocation of resources whatever the initial assignment of property-rights.” If the affected parties can contract with each other, the externality will be internalised and the party who has the legal right to control will take into consideration its effects on the other.

The initial assignment of rights does affect the distribution of income. Under a permissive law, an efficient bargaining increases the polluter’s profit by Qd and under a restrictive regime, an efficient bargaining increases it to Qa.

Despite private bargaining, inefficiency arising from externalities persist for a variety of reasons. In “small number” there may be failure to agree on the division of the gains from a move to a more efficient allocation.

In “large number” the absence of contracting between polluter and victims may arise. The free rider problem is likely to be important, because it will be difficult for the polluter to control the level of pollution for a particular victim.

Reduction in pollution will tend to benefit all victims have in the area irrespective of whether they are willing to pay or not for a reduction in pollution. In addition, the legal situation may not be well-defined, so that it is not clear whether the polluter has the legal Tight to pollute, or his victims the legal right to protection from his pollution. Legal remedy is likely to be very costly.

Even if the market is established, it may not be competitive; a single polluter confronting many victims may act like a monopolist with respect to changes in the level of pollution. There is still interest in a solution to the externality problems which require public intervention.

Pigovian Taxes and Subsidies:

If the externality cannot be internalised via a Coasian bargaining, it may be possible to mitigate the inefficiency through government action. Prof. Pigou suggested that externalities should be internalized by a suitable taxes or subsidies policy. Suppose the legal regime is permissive, so that, a polluter would choose an inefficiently high level of pollution.

Imposing a tax of t per unit on the output of pollution would give the polluter a profit function of B(x) – tx and the level of pollution chosen would satisfy B'(x) – t = 0. If the Pigovian tax rate was imposed on the marginal damage inflicted by the polluter then the efficient pollution level would be: t = D'(x*); the polluter would be allowed to choose the efficient amount of pollution, where

B'(x*) = t = D'(x*) …………. (2)

By making the polluter pay the marginal damage imposed by pollution the tax internalizes the externality:

Apart from the potential problems with Pigovian taxes, there are difficulties of obtaining the information necessary to calculate the correct rate of tax. If the parties can bargain about the level of externality, a Pigovian tax may not lead to efficiency.

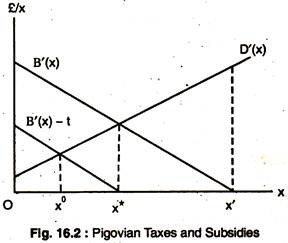
Fig. 16.2 shows that the effect of the tax is to shift the polluter’s marginal benefit (MB) curve down from B'(x) to B'(x) -1 and the polluter will maximise after tax profit by choosing x*.

But, suppose, the chemical firm and the brewery can still negotiate. At x*, the brewery still suffers positive marginal damage from pollution, whereas, the after tax MB to the polluter is zero. A bargain to reduce x to x⁰ could make both of them better-off; but the governments’ tax revenue would be reduced by l(x* -x⁰), which is larger than the private gain from the bargain.

The new allocation at x⁰ is Pareto inefficient it would be possible to increase tax revenue and make both firms better-off if x was increased from x⁰ to x*. If private bargaining is possible, efficiency can be gained without Pigovian taxes. One justification for such taxes might be the achievement of better distribution of income only.

A tax on pollution could be combined with a subsidy to those who suffer from an externality to compensate for the damage. If such a subsidy is paid, it may not provide any incentive for private bargaining between the parties. Now, suppose, out of the proceeds of tax revenue, collected from the chemical firms, the brewery was paid a subsidy equal to the amount of damage it suffers from the effluent.

Thus, the combination of a Pigovian tax and subsidy leads to efficiency, even if the parties could bargain, provided the brewery can do nothing to change the damage that it suffers.

The magnitude of the effects of damage from externalities can be influenced by the actions of both parties, not just the party who causes the externality. For example, the brewery might be able to use a different production process which requires less water or sink a well to get less polluted water.

Thus, efficiency requires that both parties mitigate the damage through a Coasian bargain. Instead, it can be shown that paying compensation to the brewery, when it can influence the costs imposed by the effluent, leads to inefficiency.

Suppose, the damage function is D(x, z) where z is the expenditure by the brewery to reduce the damage imposed on it by the chemical firm: Dz < 0. Let S(D) be the compensatory subsidy given to the brewery. The brewery will choose z to maximise S(D) -D -z and z will satisfy the Kuhn-Tucker condition :

S'(D) Dz – Dz – 1 = Dz (x, z)[S(D) – 1] – 1 < 0, z ≥ 0……………….. (3)

But, efficiency requires that B(x) – D(x, z) -z is maximised which implies that D(x, z) – 1 = 0 …………. (4)

(We assume that Dz(x, 0) > 1, if x > 0 so that it is always efficient for the brewery to undertake cost-reducing expenditure against effluent.) Comparing (3) and (4), we see that paying full compensation (S = D) to the brewery will eliminate its incentive to reduce the damage it suffers: If S'(D) = 1, the brewery will set z = 0.

In general, if the compensation varies with the amount of damage suffered (S'(d) > 0), there will be a less than efficient level of mitigation expenditure.

Common Property:

A common property resource is an asset whose services are used in production, or consumption and which is not owned by any one individual. Examples are ocean fisheries and common grazing land and public goods. We suggested earlier that common ownership can cause inefficiency and we will show this here.

Take the example of a lake in which all members of the community have the right to fish. For simplicity, let us assume that the total output or catch depends on the total time spent fishing by all individuals:

q =f(L)=f(∑L_i.)……………… (5)

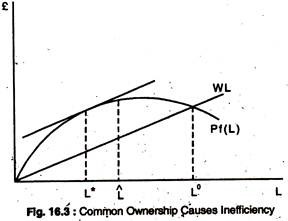
where q is the total output or catch, L_i is the time spent for fishing by the ith individual and L = ∑L_i. is total time spent fishing. f(L) is concave in L and attains a maximum at L in Fig. 16.3. The ith individual’s catch, q_i, is: q_i = (L_i/L).f(L) ………………..(6)

It is assumed in equation (6) that everyone is equally skilful and can fish anywhere in the lake. Hence, the proportion of the total catch made by ith individual is the proportion of total fishing effort of labour input: q_i/q = L_i/L. Alternatively, catch per unit of labour input is q/L and, so, L_i hours spent fishing yield a catch of L_iq/L.

We also assume that variations of total output from the lake have no effect on the price of fish, p, and that variations in the total labour input have no effect on the wage-rate. They wish to maximise their individual profits : π = pq_i – WL₁ where π is i’s profit.

Hence each sets L. so that:

P[q/L + (L_i/L) (f” —q/L)] –W = 0 ………….. (7)

With this condition each individual is maximising profit and is, in fact, earning a positive profit which is: pq_i – WL_i = (p.q/L – W).L_i, which is positive, for L_i > 0, if p. q/L – W > 0.

If the marginal product declines (f’’ < 0), marginal product f’ < q/L.

The equilibrium total labour input, L⁰, in Fig. 16.3 has the property that a reduction in total fishing effort, say to L, would actually increase total output. This occurs because the wage-rate is low enough for an intersection to take place in the range of negative marginal products.

The outcome, in this case, will be inefficient as long as the output of fish has a positive value and labour devoted to fishing has an opportunity cost. In order to generalize this result, we have to make some assumptions about the marginal social value of fish and the marginal social cost of labour.

We assume that these are, in fact, measured by the market prices offish (p) and labour (W), respectively. Hence net social benefit from fishing in the lake is: pq – WL, which is maximised when pf’-W= 0………….. (8)

In terms of Fig. 16.3, the efficient level of L is L* where the vertical distance between the pq and WL curves is greatest. Notice that L* is always less than L° since f’ < q/L: Free access always leads to overfishing if there are diminishing returns which means that the intersection of WL and pf(L) in the figure always occurs at a value of L greater than that at which their slopes are equal.

The efficient outcome could be achieved if all the individuals with fishing rights can agree to reduce their total labour to L*. Such an agreement may not be very likely if there are a large number of individuals with fishing rights or if it is difficult to police such an agreement because breaking the agreement would be profitable.

One solution could be to divide the lake among the individual fishermen and give each of them exclusive right to fish in that part of the lake. These rights will require policing and enforcing and this may be expensive.

An alternative solution would be to vest ownership of the lake in the individual. Since, on our assumptions, total profit from fish production from the lake is the net social benefit, maximisation of profit leads to efficient labour input.

Unrestrictive access leads to intensive use, but it may also lead to other kinds of inefficiency because it weakens the incentive of individual decision-makers to invest in improvements to the productivity of the resource, or to pay regard to the possibility of extinction of the fish stock through overfishing.

Since a single individual cannot prevent others from using the resource; the benefits from investment or voluntary restraint will be spread over all other users.

Hence, it will not pay any single decision-maker to undertake the investment, or to restrict his catch, even though the total benefits exceed the cost. Even if the share of the benefits accruing to a single individual exceeds the cost of the investment, it may not be undertaken if each individual believes that he will benefit from the investment of other users.

Because of non-excludability, investment by other users is a substitute for investment by any particular individual and if all individuals realize this, no investment may take place.

The market fails in this case because no market can exist in the absence of well-defined and easily enforceable rights to exclude by any single individual. There is nothing which can be exchanged and no means which individuals can capture or be made to bear all the results of their actions.

Public Good:

The defining characteristic of a public good is that it is non-rival and non-exclusive: Consumption of it by one individual does not actually or potentially reduce the amount available to be consumed by another individual. Examples include radio and television broadcast and national defence.

Any individual can listen to or watch the output of a broadcasting station, without preventing any other individual who possesses a radio or television receiver from consuming the same output.

Any individual can increase his consumption of television broadcasts up to the total number of hours broadcast, without reducing any other individual’s actual or potential consumption. Broadcasts are an example of an optional public good, in that, one can choose to consume any amount of output produced.

Defence is a non- optional public good in that all inhabitants of the country consume the total quantity provided; and if one inhabitant is to be defended, all will be.

In the case of non-optional public goods, if we denote the total quantity produced by q and the total quantity consumed by the ith individual by q₁, i = 1,………….n, we have q₁ = q₂ = ……….q_n = q ………….(9)

On the contrary, private goods are the goods which have the characteristic that with a given output, an increase in one individual’s consumption of a private good reduces the amount available for consumption by other individuals.

Note that an increase in one individual’s consumption of a private good need not actually reduce the level of consumption by any other individual, but only the amount available to be consumed by others.

For example, if I occupy a seat in an empty railway compartment, my consumption of the railway travel will not reduce that of anyone else’s but it reduces the availability of consumption to one other since I have occupied one seat.

For private goods, the relationship between individual consumption x_i and output X is:

x₁ + x₂ +……………+ X_n < x_p ………….. (10)

Efficiency with Public Goods:

We derive the necessary conditions for Pareto efficiency in a two-person, two-good economy.

The preferences of consumer i can be represented by the quasi-linear utility function:

Uⁱ(x_i, q) = B_i(q) + x_i

B_i > 0,B”_I < 0, i = 1,2 ………….. (11)

where q is the consumption of the non-optional public good by consumer i and x is consumption of the private good. The MRS of consumer i MRSⁱ_xq= U_q /U_x = B’_i, which is the marginal valuation of the public good by i in terms of the private good.

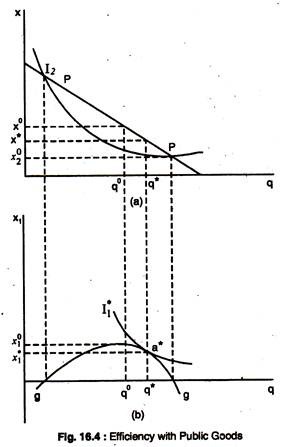
Notice that the assumption that preferences are representable by a quasi-linear utility function means that the marginal valuation of the public good is independent of the amount of the private good consumed. The production possibilities for the economy are shown in Fig. 16.4(a). The production possibility frontier, PP, is a straight line so that MRT_xq = C, indicating that we are assuming that the public good has a constant MC in terms of forgone private good output. We derive the efficiency conditions by maximising U¹ subject to individual 2 at least getting a specified level of utility U² and subject to the material balance constraints and technology.

In such an economy, the feasible output combinations are those on or below PP and material balance constraints. Since consumer 1 is non-satiated, the constraint on U² and the material balance constraint on the private good will bind as equalities in an efficient allocation.

The IC I₂ in Fig 16.4(a) shows combinations of x₂ and q which satisfy the utility constraint U² (x₂,q) = U². The vertical distance between PP and I₂ shows, for any level of q, the maximum amount of the private good which can be consumed by individual 1 given the technology of economy and the constraint that U² = U².

For example, when q = q⁰, the maximum amount of private good available for individual 1 is x⁰₁ = x⁰ – x⁰₂. Thus, since individual 1 will also be able to consume public good, his consumption bundle is (x⁰₁, q⁰) when the public good output is q⁰.

The curve g in Fig. 16.4(b) shows the vertical distance between PP and I₂ which gives the feasible consumption bundles of individual 1 provided that individual 2 has utility U². Utility of individual 1 is maximised at a* where his indifference curve is tangent to g. Since the slope of g is the difference between the slope of PP and the slope of I₂:

(MRT_Xq – MRS²_xq) and the slope of I*1 is -MRS²_xq, the efficient allocation is characterised by:

(MRS¹_xq + MRS²_xq)= MRT_xq ………… (12)

or, marginal benefit = marginal cost, which, in terms of single specification of preferences and technology,

B’₁(q)+B’₂(q)=C……………. (13)

Because q is a public or non-rival and non-exclusive good, an increase in q by one unit increases all individuals’ consumption of the public good by one unit. Hence, the marginal value of the additional unit of the public good, in terms of the private good, is the sum of all the individuals’ marginal valuations of the public good.

Efficiency requires that the amount of the private good the individuals would be willing to give up to acquire an extra unit of the public good (I.MRS must be equal to the amount by which production of the private good must be reduced to raise the output of the public good by one unit (MRT_xq).

A market economy is unlikely to satisfy the efficiency conditions for the supply of public good for two reasons First, many public goods are non-excludable. For example, defence and police services. If it is impossible to exclude non-payers from consuming a public good, firms may not be able to collect revenue to cover the cost of producing the public good.

If there are free riders because they cannot be excluded, the price that firms charge for supplying a public good may not be an adequate measure of the marginal benefit of the good and there will be a less efficient supply of the good.

Second reason is that the market may fail to provide an efficient amount of public goods even when they are excludable, arising from another characteristic of public goods: non- rivalry.

Suppose, a good is excludable, transferable, there are many consumers and producers and also low information costs. In such a situation, if the good is private, the resulting market equilibrium allocation will be optimal.

Competitive market economy ensures that all consumers pay the same price, which will be equal to the marginal cost of the good in each of the firms. Consumers will compete for a given output of the good and no consumer will be offered or be able to force a sale at a price less than the market price.

By contrast, if the good is public, even if excludable, the opportunity cost of a unit sold to one consumer is zero when output q is given. Since the good is a public good, an additional unit consumed by one individual does not reduce the amount available for consumption by any other individual. This means that no consumer is competing against any other consumer for a particular unit.

The consumer, and, thus, the market is not competitive, despite the large numbers of buyers and sellers. If a consumer realizes that the marginal cost of his own consumption is zero, he may offer to the producer a very low payment for the right to consume the producer’s output. If all consumers act in this way, the amount offered by consumers will be. insufficient to cover the costs of production — and a zero output will be produced.

In a competitive market for a private good, consumers realise that they cannot affect the market price and, hence, they adjust their consumption until their marginal valuation of the private good is equal to its price. Hence, all consumers’ marginal valuations are equal to the price, and in a competitive market, P = MC, and the efficiency conditions for private goods will be satisfied.

In a market for a public good consumers’ marginal valuations of the good, will generally differ and, so, each should be charged a different price equal to his marginal valuation. The sum of these prices should then be equated to the MC of the public good. Consumers have no incentive to reveal correctly their marginal valuations of the public good since they do not regard the prices as unalterable, and, so, will not be satisfied.

Public Goods and Market Failure:

Suppose, we are deciding to introduce a mosquito abatement programme for the community. We know that the programme is worth more to the community than the private cost of £50,000 required to provide it. Can this programme be privately provided? We would probably break even if we can introduce a fee of £5 to each member of 10,000 households in our community.

But we cannot force them to pay the fee, let alone devise a system in which those households that value the programme the most pay highest fees.

The problem is that mosquito abatement is non-exclusive — there is no way of providing the service without benefiting everyone. Thus, households do not have the incentive to pay what the programme is really worth to them. People can act as free riders, understanding the value of the programme so that they can enjoy its benefit without paying for it.

With public goods, the presence of free riders makes it really difficult — or even impossible for markets to provide goods efficiently. Perhaps if few people were involved and the programme were relatively inexpensive, all households might voluntarily agree to share its costs.

However, when many households are involved, voluntary private arrangements are usually ineffective, and the public good must be subsidized or provided by governments, if it is to be provided efficiently.

Private Preferences for Government-Produced Public Goods:

Government provision of a public good is advantageous because the government can spend money from the revenue and increase taxes to pay for it.

But how can the government determine how much of a public good to provide when the free rider problem gives people the incentive to misrepresent their preferences? Here we discuss how to determine the private preferences for goods that the government provides and/or produces.

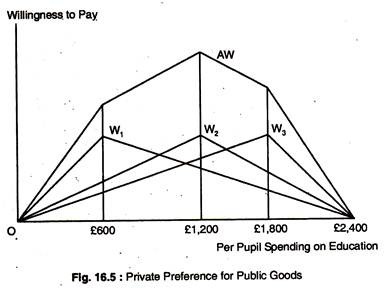
Majority voting rule is commonly used to decide allocation questions. Let us examine here how majority voting rule determines the provision of public education. Fig. 16.5 describes the preferences for spending on education of three citizens who are representatives of three similar groups of people in the school district.

Curve W₁ gives the first citizen’s (first group of citizens) willingness to pay for education, net of required tax payments. In general, the benefit from education increases as spending increases which requires increased tax payments as well. The willingness to pay curve initially slopes upward because the citizen places great value on low-spending levels.

However, when spending increases beyond £600 per pupil, the value on education increases at a diminishing rate, so the net benefit actually declines. Eventually, the spending level becomes so great (£2,400 per pupil) that the citizen is indifferent between this spending and no spending.

Curves W₂ and W_3, representing the second and third citizen’s willingness to pay, are similarly shaped but reach maximum at £1,200 and £1,800 per pupil, respectively. The solid line AW represents the aggregate willingness to pay for education — the vertical summation of the W_1, W₂ and W₃ curves.

The AW curve provides a measure of the maximum amount that all three citizens are willing to pay to enjoy each spending level. As the figure shows, the aggregate willingness to pay is maximised when £1,200 per pupil is spent because this measures the benefit of spending net of tax payments required to pay for that spending and this also represents the efficient level of spending.

Will majority voting achieve the efficient outcome? Suppose the public is required to vote whether to spend £1,200 or £600 per pupil.

The majority will vote for £1,200 per pupil (two against one) which represents the most preferred alternative of the median voter. Under majority rule voting, the preferred spending level of the median voter will always win an election against any other alternative.

However, majority rule voting allows the preferences of the median voter to determine referenda outcomes, but these outcomes need not be economically efficient. Majority rule voting is not always efficient because it weighs each citizen’s preference equally — the efficient outcome weighs citizens’ vote by their strength of preference.

Public Good:

We have seen that externalities create market inefficiencies that sometimes warrant government intervention and/or regulation. When should the government replace private firms as the producer of goods and services? Here we describe a set of conditions under which the private market either may not provide the good at all or may not price it properly once it is available.

Public goods have two characteristics: They are non-rival and nonexclusive. A good may be regarded as non-rival, if, for any given level of production, the marginal cost of providing it to an additional consumer is zero. For most privately provided goods, the marginal cost of producing an additional good is positive.

But for some goods, additional consumers do not add to cost. For example, a highway during a period of low traffic volume, because the highway already exists and there is no congestion, the additional cost of driving extra traffic (cars) on it is zero. Or, consider the use of public television. Once the television is in operation, the cost of providing it to one more viewer is zero.

Most goods are rival in consumption. For example, when we buy furniture, we rule out the possibility that someone else can buy it — thus, the furniture is a rival good. Rival goods are required to be allocated among individuals, whereas non-rival goods can be made available to everyone without affecting any individual’s opportunity for consuming them.

A nonexclusive good is one if people cannot be excluded from consuming it. As a consequence, it is difficult, if not impossible, to charge people for using nonexclusive goods the goods can be enjoyed without directly paying for them. For example, national defence is a nonexclusive good.

Once it is provided, no one can be excluded from its benefit. Other examples of nonexclusive goods are public television, lighthouse etc.

Some goods are non-rival but exclusive. For example, in periods of low traffic, travel on the bridge or highway is non-rival because an additional vehicle on the bridge or highway does not lower the speed of other vehicles. But it is exclusive because the authorities can keep people from using it.

A television signal is another example of a non-rival good. Once the signal is broadcast, the marginal cost of making the broadcast available to another user is zero, so it is non-rival. But broadcast signals can be made exclusive by scrambling the signal and charging for the code that allows it to be unscrambled, thus, a company can exclude users.

Some goods are nonexclusive but rival. Air is nonexclusive but can be rival if the emissions of one firm adversely affect the quality of the air and, thus, deny other people from enjoying it. A lake or ocean is nonexclusive, but fishing is rival because it imposes costs on others.

Public goods — which are both nonexclusive and non-rival — provide benefits to people at zero marginal cost, and no one can be excluded from enjoying them. For example, national defence is a public good which is nonexclusive and is also non-rival. The lighthouse is also a public good, because, it is non-rival and nonexclusive.

Many publicly provided goods may not be public goods but they are either rival in consumption, exclusive, or both. For example, school education is rival in consumption because there is a positive marginal cost of providing education to one more child.

Similarly, charging tuition fee can exclude some children from enjoying education. Education is provided by the government because it entails positive externalities, not because it is a public good. Lastly, consider the management of a national park. Some people may be excluded from using the park by raising entrance fee. Use of the park is also rival — because of crowded conditions.