Shift and Rotation of the Budget Line (With Diagram)

In this article we will discuss about the shift and rotation of the budget line, explained with the help of a suitable diagram.

In the indifference curve theory, it is assumed that the consumer purchases and consumes only two goods (here X and Y). If the prices of goods X and Y, and the money income of the consumer is given, then the equation of the budget line of the consumer would be

M̅ = p_x.x + p_y.y                               [eqn.(6.15)]

The slope of the budget line (6.15) is –p_x/p_y = negative, and x-and y-intercept of the line are M/p_x and M/p_y, respectively.

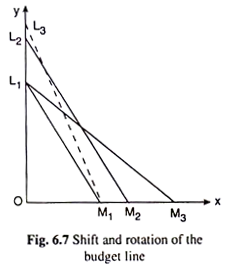
Now suppose, initially the values of M, p_x and p_y are such that the budget line of the consumer has been obtained to be a line like L₁M₁ in Fig. 6.7.

If now the money income (M) of the consumer rises, p_x and p_y remaining unchanged, then, the slope (-p_x/p_y) of his budget line remaining constant, the intercepts of the line (M/p_x and M/p_y) would increase.

As a result, the budget line would have a rightward parallel shift from L₁M₁ to a new position like L₂M₂. Conversely, if the money income of the consumer decreases, prices remaining constant, the budget line would have a parallel shift to the left. This rightward or leftward parallel shift of the budget line is known as “shift” of the budget line.

On the other hand, if the money income of the consumer remaining constant, the price of one of the goods changes, then it is known as the “rotation of the budget line”. For example, suppose, initially, the consumer’s budget line is L₁M₁ in Fig. 6.7.

Now if the money income (M) of the consumer and the price of good Y remaining unchanged, the price of good X diminishes, then the y- intercept of the budget line (M̅/p_y) remains constant at OL₁, but the x-intercept (M̅/p_x) increases from OM₁ to, say, OM₃.

As a result, now the budget line of the consumer would be L₁M₃. Here the budget line while changing its position from L₁M₁ to L₁M₃, rotates anticlockwise about the point L₁. This is known as the “rotation” of the budget line.

Similarly, if M and p_x remaining constant, p_y falls, then also a rotation of the budget line from the initial L₁M₁ position to a position like L₃M₁. Now the x-intercept of the budget line remaining constant, the y-intercept increases and the rotation of the budget line would be clockwise about the point M₁.