Calculating Calculate MPC and APC from the Consumption Function

The following article will guide you to learn how to calculate MPC and APC from the consumption function.

According to A. H. Hansen, the consumption function is ‘the heart of the Keynesian analysis’.

The consumption function—’the propensity to consume’ in Keynesian terminology—was a fundamental component of the General Theory (1936). That hypothesis states that consumption expenditures are a function of current personal disposable income: C=f (Y), where consumption (C) is a function of (or, consumption depends upon) income (Y).

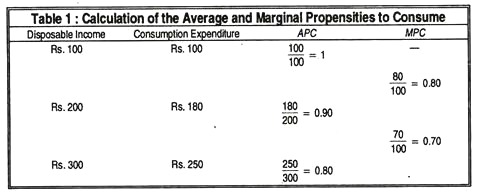
Keynes stated that if income increases, consumption will also increase but not proportionately. For example, if disposable income (i.e., money income less taxes paid) of an individual increases by Rs.100, consumption may increase by Rs.80.

Here change in consumption induced by a change in income is called the marginal propensity to consume: ΔC/ΔY, where Δ denotes any change. In our example it is 80/100=4/5=0.80. Total consumption divided by total income gives the average propensity to consume.

Keynes thought that marginal propensity to consume is less than average propensity to consume as Table 1 shows:

In a country like India where per capita income is very low, we can assume, additionally, that at some low level of income consumption would exceed income. As income increases, expenditure on consumption goods falls. So, saving may increase.

Now, it is believed that people’s consumption and, thus, saving are influenced by their wealth as well as by their current income. In the short run, wealth is fairly constant, but over a long period it will rise and will make long-run consumption higher from a given level of income than in the short-run. So, consumption is a function partly of income and partly of wealth.

According to Keynes, total income is the sum total of consumption and saving. Since total income is fixed, what is not consumed is automatically saved. The volume of saving depends not only on income but also on the propensity to save. It is the change in saving due to change in income.

And the sum of MPC and MPS is unity, since total income is partly consumed and partly saved. So, if MPC=4/5, MPS=l/5. In other words, if income increases by Rs.100, and consumption by Rs.80, saving must increase by Rs.20.

Keynes asserts that consumption is a stable function of income. Regard­ing the relationship between consumption and income on the individual (as also on the aggregate) level, Keynes put forward four important proposi­tions:

(1) Real consumption expenditure is a stable function of real income;

(2) The MPC is positive, but less than one (if MPC=1, MPS would be zero);

(3) The MPC is less than the APC (which implies that the latter declines with rising income); and

(4) The MPC itself declines as income rises.

According to R. G. Lipsey, two basic hypotheses provide the core of the Keynesian theory of consumption function:

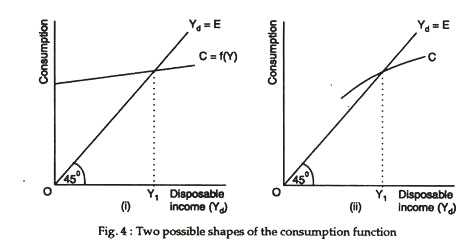
(1) There is a break-even level of income at which APC=1. Below this level, APC is greater than unity and above it APC is less than unity.

(2) The MPC is greater than zero but less than all unit levels of income.

These two points are illustrated in Fig. 4. So, there are two possible shapes of the consumption function. In Fig. 4(i) the MPC is constant but APC declines as income rises. In Fig. 4(ii) both the APC and the MPC decline as income rises.

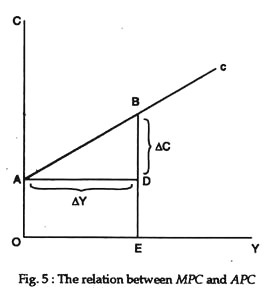
It may be noted, if the consumption function has an intercept (i.e., an autonomous component as in Fig.5, MPC will be less than APC even if MPC is constant. Here MPC = BD/AD = BD/OE since AD = OE.

But BE/OE. Since BD < BE, BD/OE < BE/OE or, MPC<APC.

This may also be shown thus:

The Keynesian consumption function equation is expressed as C = a + bY where a is autonomous consumption and b is MPC (the slope of the consumption line).

Here, APC = C/Y = a/Y + b

Since, a > 0 and y > 0, a/Y is also positive. Here, MPC < APC.

Long Run Consumption Function:

According to Keynes, the APC—the ratio of consumption to income—falls as income increases. This happens in the short run when MPC < APC. But history shows no tendency for MPC to fall in the long run as all households become richer.

In the long run MPC remains constant and is equal to APC. This has been proved by three economists, viz., James Duesenberry, Milton Friedman and Franco Modigliani who put forward there alternative hypothe­ses regarding long-run consumption behaviour, viz., the relative income hypothesis, the permanent income hypothesis and the life-cycle hypothesis.

These three hypothesis are briefly discussed below:

1. The relative income hypothesis:

In 1949 James Duesenberry devel­oped the relative income hypothesis. He suggests that an individual’s consumption depends not on his absolute income (as has been postulated by Keynes) but on his relative income, i.e., current income in relation to income to which he is accustomed (his previous peak income or the maximum income that he earned in the past).

Thus, when, during depres­sion, income falls consumption expenditure does not fall much. Instead, an individual tries to maintain the same level of consumption either by borrowing or by reducing his accumulated balances. On the other hand, when, during economic prosperity, income increases consumption spending does not in­crease much.

Rather the major portion of additional income is utilised to repay an old debt or to restore the old saving rate. It so happens because an individual finds it very difficult to curtail his consumption than to raise it. This is known as the ratchet effect.

Thus, the basic point made by Duesenberry is that, in a particular phase of the business cycle the relation between income and consumption is one of non-proportionality. But, over the entire business cycle the relation is one of the proportionality. This again means that the MPC is constant in the long run and is thus equal to APC.

2. The permanent income hypothesis:

Milton Friedman’s permanent income hypothesis (1957) suggests that, both income and consumption are divided into two parts, viz., permanent and transistory.

Permanent income is expected future income of an individual over his life time. It depends on a consumer’s total wealth or capital assets which includes both physical assets and human capital (i.e., educational qualifica­tion or training acquired at a cost).

His total wealth determines his ability to earn the annual figure for permanent income can be calculated by dividing the total expected income of a consumer by his life expectancy in years. Transistory income reflects all other factors that occur through chance or accident, such as windfalls (e.g., winning a bet or a lottery) or negative transistory income resulting from illness.

Permanent consumption is comparable to permanent income. It includes expenditure on mortgage repayments, heating, lighting and the like. Tran­sistory consumption is that part of total (measured) consumption which is not permanent, for example purchasing a second car out of windfall inheri­tance or unplanned purchase of an article like an ornament one’s eyes.

Friedman argues that, transistory components of income and consump­tion are uncorrelated with their permanent components (and are uncorrelated with each other). But, there is a proportional relation between permanent income and permanent consumption. This is possible when MPC is constant and in the long run is equal to APC.

3. The life cycle hypothesis:

In the early 1950s Franco Modigliani origi­nated the ‘life cycle hypothesis’ of consumption. This hypothesis suggests that individuals save during their earning years and ‘dis-save’ after retire­ment. The main argument put forward by Modigliani is this: although all household income is consumed over the life cycle, a growing economy generates a positive amount of saving because young savers are richer and more numerous than retired dis-savers; given some assumptions about population growth and life expectancy this argument yields a constant historical ratio between saving (consumption) and income. Thus, as in Friedman’s hypothesis, if the relation between income and consumption is one of proportionality MPC-APC in the long run.