Keynes’ and Kuznets’ Consumption Function

Let us make in-depth study of the Keynes’ consumption function and Kuznets findings of consumption function puzzle.

Keynes’ Consumption Function:

Empirical studies of long-term time series data of the US economy for the period 1869-1938 made by the noted American economist Kuznets.

He estimated a consumption function which contradicts Keynes’ consumption function which was found to be correct on the basis of cross-section studies of household budget data and short-term time series data.

This contradiction between Kuznet empirical findings and Keynes ‘consumption function has been called consumption function puzzle. Efforts have been made by several economists to resolve this puzzle and new theories of consumption function have been put forward to resolve the conflict between Keynes’ consumption function and Kuznets’ findings.

To compare the Keynes’ and Kuznets’ consumption functions, it will be useful to write them in algebraic form and graphically represent them.

Keynes’s consumption function can be algebraically written as below:

C = a + bY ….. (1)

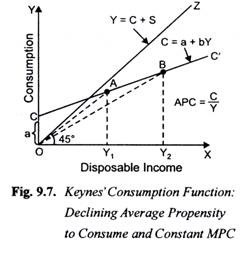
where a is a positive intercept term which is also called autonomous consumption as it does not vary with income. The constant a shows that even when income is zero, a certain consumption is present. This is possible when in any year a community can live either on its past savings or borrow from other communities. Keynes’ consumption function is shown in Fig. 9.7.

Secondly, b in the consumption function represents marginal propensity to consume (∆C/∆Y). The above mentioned Keynes’s consumption function (C = a + bY) shows that average propensity to consume(C/Y) falls as income increases. This can be known by comparing slopes of the rays OA and OB at income levels Y₁ and Y₂ respectively in Fig. 9.7.

Kuznets’ Consumption Function:

On the other hand, Kuznets found that consumption function is of the following form:

C = bY … (2)

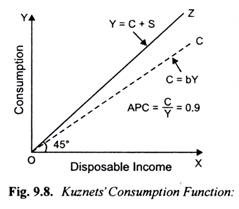
In Kuznets’ consumption function there is no intercept term (that is, autonomous consumption). This is shown in Fig. 9.8 where it will be seen that Kuznet’ consumption function curve starts from the origin and is very near to 45° line depicting that the propensity to consume (b) is very high.

From his empirical study Kuznets estimated that average propensity to consume was nearly 0.9. Besides, by dividing the entire period (1869-1933) into three overlapping 30 years sub-periods Kuznets found that the proportion of consumption to income (that is, average propensity to consume) was nearly the same and equal to about 0.87 in all the three sub-periods.

Thus Kuznets concluded that there was no tendency for the average propensity to consume to decline as disposable income rises. Thus, rounding off Kuznets estimated propensity to consume is equal to 0.9.

His consumption function presented in equation (2) can be rewritten as:

C = 0.9 … (3)

Keynes’ consumption function (C = a + bY) and Kuznets’ consumption function (C = bY) are different. Whereas in Keynes’ consumption function A PC falls as income rises, in Kuznets ‘consumption function it remains constant over a long period. Further, the value of marginal propensity to consume which is less than one is much higher in Kuznets’ function as compared to that of Keynes.

The reconciliation between two types of consumption functions has been made by some economists by pointing out that whereas Keynes’ function is short-run consumption function, ‘Kuznets’ function is concerned with long run and is referred to as long-run consumption function.

In the long run, short run consumption function curve shifts above and therefore in the long run consumption function, propensity to consume, is higher as compared to that in the short run. Further, Friedman’s permanent Income Hypothesis and Modigliani’s Life Cycle Hypothesis have also tried to reconcile the two functions by referring to the short-run and long-run consumption behaviour of the people.