Difference between Slope of Demand Function and Elasticity of Demand

This article will help you to learn about the difference between slope of demand function and elasticity of demand.

Difference between Slope of Demand Function and Elasticity of Demand

By slope of the demand function we mean change in price divided by the change in quantity. Let P = f (Q) be the inverse demand function. Thus, the slope of the demand function

= absolute change in price/absolute change in quantity = ∆P/∆Q

Again, slope refers to the steepness of the demand curve. In fact, slope of the demand function measures the steepness or flatness of the function.

On the other hand, elasticity of demand measures the relative change in price and quantity. Thus

E_P = ∆P/∆Q. P/Q

Elasticity of demand is the reciprocal of the slope of the demand function, multiplied by the price-quantity ratio, i.e.,

E_P = 1/∆P/∆Q. P/Q= -∆Q/∆P. P/Q

Thus, the slope and elasticity of demand are related but are not the same thing. Simply by studying the slope of the demand function, one cannot determine the value of elasticity of demand, though it is said that steeper (latter) the demand curve lower (higher) is the elasticity of demand.

This is a wrong conception. In fact, there is no connection between the slope and the elasticity of demand. It may happen that the two demand curves may have different slopes but the same elasticity or the two demand curves may have same slopes but different elasticities.

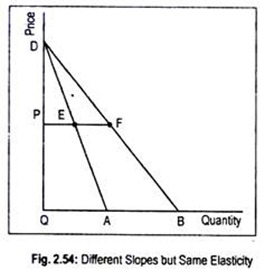
In Fig. 2.54, we have drawn two demand curves labeled as DA and DB. These two demand curves have the same intercept from the price axis, but they exhibit different slopes. In fact, the curve DA is steeper than DB. So elasticity of demand at any point on the DA curve should be less than that of the demand curve DB. But this is not so. This can be verified in the following way.

Consider two points E and F on the two demand curves having the same price OP. Elasticity of demand at point E on the curve DA is

EA/ED = OP/PD

Similarly, elasticity of demand at point F on the demand curve DB is

FB/FD = OP/PD

Thus, elasticity at point E = elasticity at point F. This suggests that though slope differs, elasticity is the same for the two demand curves at each price.

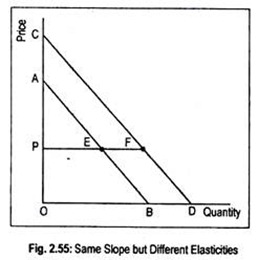
Fig. 2.55 shows that the two demand curves may have the same slopes but different elasticities. Being parallel, two demand curves AB and CD have the same slopes. Now consider points E on the demand curve AB and F on the curve CD. Now consider price OP. Then elasticity of demand at point E on the demand curve AB is

EB/EA = OP/PA

Again, elasticity of demand at F on the curve CD is

FD/FC = OP/PC

It is clear from the figure that since PC >PA

OP/PC = OP/PA

Thus, elasticity at point F on the curve CD is less than the elasticity at point E on the curve AB. Alternatively, in Fig. 2.48, point E may be assumed as the mid-point on the curve AB corresponding to the price OP. Thus, at that point, elasticity of demand is equal to one. But F on the demand curve CD at the price OP lies below its mid-point. So, elasticity at F must be less than one.

Thus, slope and elasticity of demand are not the same thing.