The problem of choosing an appropriate technique of production or technology arises when the LDCs have already decided on a particular project. Choosing between the alternative methods of production is one of the major problems that confront development planning.
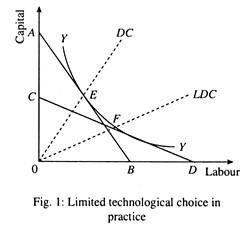
If labour (L) is more abundant and capital (K) scarcer in LDCs we might expect to see the use of more labour intensive techniques of production in the modern industrial sector. Figure 1 compares the techniques of production that should be found in LDCs with that found in DCs.
Assuming the same production function in the two sets of countries represented by the isoquant labelled YY, the lower price of labour relative to capital is given by the isocost ab and the higher relative price given by ed. D Labour The two isocost lines give the relative prices of labour to capital in LDCs and DCs, respectively.
ADVERTISEMENTS:
In the developed countries K/L ratio is given by the ray from the origin labelled DC and that for the LDCs is given by the one labelled the same. ADC and LDC differs in technique of production mainly in the aggregate sense as large sectors of an LDC use very little capital such as subsistence farming and petty service activities.
In the modern sector, however, techniques are more capital-intensive-1 in an LDC than what would be predicted on the basis of factor endowments. The judgments passed on the basis of the latter would advocate a more capital-intensive-1 technique to be “appropriate” for a capital-rich developed economy and that an capital-intensive technique would be more appropriate for a LDC. So, why is this “inappropriate” technique applied to most LDCs?
There are several reasons that are discussed below:
ADVERTISEMENTS:
(a) Factor Price Distortion:
In a labour surplus economy L is the abundant factor and K is the scarce factor, and we expect the former to be cheaper than the other, but in a lot of LDCs this is not the case. The wage rate is bid up and the interest rates are kept deliberately low. Such a price ratio does not reflect the relative factor endowments of a LDC and what has occurred is factor-price distortion.
ADVERTISEMENTS:
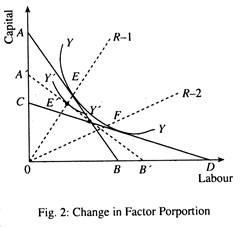
In Fig. 2 a DC would follow the path R—1 of high capital intensity and a LDC should normally follow R-2 with low capital-labour ratio. Suppose the price of labour in an LDC is bid up and the rate of interest is lowered, the distorted isocost line is A’B’ which meets a new isoquant Y’Y’ on the path R-1 indicating capital-intensive production in a labour-surplus economy. The rationale behind this “inappropriate” technology is the profit motive of the cost-conscious profit-making private enterprises.
(b) Efficiency Wage:
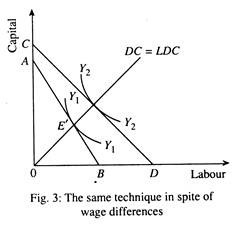
An important factor behind the use of capital-intensive technology (KIT) in an LDC is the high efficiency wage though labour may be abundant and its money wage may be lower than in a DC but is not necessarily “cheaper” or less costly to employ because MPL may be lower too. The efficiency wage = nominal wage/ APL may differ very little between LDCs and DCs. This discourages private entrepreneur from increasing employment, instilling a tendency to save and use KIT.
In Fig. 3 the production function for an LDCs is labelled Y2. Even though labour is cheaper in a LDC, slope of isocost’ line for LDC (AB) is less than the slope of isocost for DC (CD), the most profitable KJL ratio will be-the same for both countries and lie along the path OE’. In an LDC it is an efficiency wage that matters and not the money wage.
(c) Limited Factor Substitutability:
For a large number of commodities that may not be a spectrum of techniques to choose from. The production function may not be a smooth one as shown in Fig. 1 and a country cannot move from E to F in accordance with differences in relative factor endowments the production function can take the L-shaped form (called Leontief production function which assumes no factor substitutability), and AT and L have to be combined in fixed proportion to get a certain level of output. Thus, the coefficients of production become fixed in such areas of production dictated by a given technology.
This naturally makes the choice of technique invariable in favour of say, when the price of labour is higher than the price of capital and accounts for the K-intensive choice of technique in an LDC. Note that here we are talking about profitable techniques. LDC might be able to utilise more Labour Intensive Technology (LIT) but then the output would not be saleable profitably.
(d) Capital an—A Substitute for Skill:
ADVERTISEMENTS:
Capital intensity in LDCs can also be explained by a skill constraint. Typically, LIT requires a great deal of skilled labour compared to KITs which require a preponderance of semiskilled labour to undertake routine repetitive tasks. In developing countries short of skilled manpower, capital may substitute for skills and constitute a rational response on part of the decision makers, whoever they may be.
(e) Import of Technology:
There is an absence of large spectrum of techniques of production. Perhaps the overriding factor which accounts for the relative capital-intensity of the developing countries is that many, if not most of the techniques are imported from abroad which, naturally, have a heavy bias in the L-saving direction. The techniques could be imported by the indigenous firms or as increasingly seems to be the case, by large foreign multinational corporations which invest in LDCs and bring their technology with them.
In this case, the technology might be inappropriate not because there is not a spectrum of techniques but because the technology available is circumscribed by the global profit maximising motives of the companies investing in LDCs. The L- saving bias of the technology is to be explained by the L-saving bias of the technological progress in the advanced countries where labour is relatively scarce and expensive.
ADVERTISEMENTS:
(f) Need for Infrastructure:
Choice in favour of a KIT may be sometimes stated by the goals of economic development. A developing economy in its initial stages requires a strong infrastructure consisting of power, transport, irrigation projects etc. that are dependent on KIT in order to build up the base of the economy. Similarly, a view to maximise long run rate of growth by maximising investment rate calls for generating maximum reinvest able surplus which is possible in more KITs than in labour intensive ones.
The state may concentrate on some heavy industries and the capital goods sectors that “creates large reinvest able surplus, external economies and builds up infrastructure of an economy. Such a state relies on KIT for production.
The points (a) – (f) help in explaining why a labour surplus LDC often utilizes K1 methods of production in their modern sector. One of the major problems of development planning is that of choosing between alternative techniques of production.
ADVERTISEMENTS:
The number of alternatives that are open to a developing country is quite often large and the amount of capital per unit of labour (i.e., capital-intensity) varies widely from technique to technique. We also note that different techniques often simplify quite different strategies of development with very different effects on the performance of the economy. To be specific, choice of technique is related to the objective of planned economic development.
In this context we can identify two different objectives:
1. Maximisation of current output or current consumption,
2. Maximisation of the rate of growth of output.
In fact, a conflict can arise between these two objectives from the point of view of choice of capital intensity. In what follows we present Amartya Sen’s model to show the nature of conflict involved in the different objectives of economic development.
First we make some basic assumptions as regards the type of economy under consideration. The economy is over populated in the sense that there exists a reserved army of labour.
ADVERTISEMENTS:
Moreover, the economy is divided into two sectors:
(a) Modern Sector
(b) A Primitive Rural Sector.
The modern sector is subdivided into two departments—Department 1 producing only capital goods and Department 2 producing consumer goods by using both labour and capital.
Moreover, it is assumed that the means of production in the modern sector are owned by the state. However rural sector is run by the family based private enterprises.
There are two classical assumptions made in the model:
ADVERTISEMENTS:
1. The real wage is fixed in terms of consumer goods and the wage bill is entirely consumed.
2. The surplus is entirely reinvest able. Moreover it is assumed that there is no technological progress. Here the choice of technique refers to the choice of capital intensity in the modern sector. The following diagrammatic illustration explains the potential conflict between employment maximisation and growth maximisation.
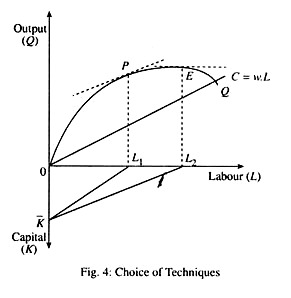
In Fig. 4 there are three axes—OY’ representing investable surplus which in fact represents output produced in Department 1. OX representing the employment in Department 2.
Let us start with a given amount of investable surplus OK. The production function exhibits diminishing marginal product of L such that with increasing capital intensity, the productivity of labour in Department 2 rises wL represents the wage bill, corresponding to different levels of employment in Department 2. Since real wage is a constant, wL is a straight line. Point E represents the maximum output and the capital intensity is represented by tan ∑KL2O.
On the other hand P is the point of maximum surplus of consumption of goods over its consumption as the slope of the curve OQ at that point equal to slope of wL, i.e., real wage rate is equal to MPL a condition for profit maximisation.
ADVERTISEMENTS:
Assuming that the entire saving comes from profit-income and it is entirely reinvested we immediately get that higher capital-output ratio, i.e., more intensive method of production generates higher profit share, higher saving rate and, thus, higher rate of growth.
Clearly, maximisation of employment requires labour intensive technique while maximisation of future growth potential necessities capital intensive technique.
The following simple algebraic formulation explains this conflict. Let the production function be:
Q-aL- bL2 … (1)
where notations have their conventional meanings and the saving function as:
S= aL-bL2 – wL … (2)
ADVERTISEMENTS:
The level of employment which maximises saving is obtained by differentiating equation (2) w. r. t. L and setting equal to zero which gives
dS/dL = a-2Lb-w = 0
Therefore, the level of employment which maximises saving is L1 = (a + w)/2b
The level of employment which maximises output is obtained by differentiating equation (1) w. r. t. L and setting equal to zero which gives
dQ/dL = α – 2bL =0
or, L2 = a/2b
The maximisation of output corresponds to the rate of turnover and the SMP criterion. On the other hand, surplus maximisation corresponds to the rate of surplus criterion (or MRTS criterion).
An interesting possibility is represented in diagram 5
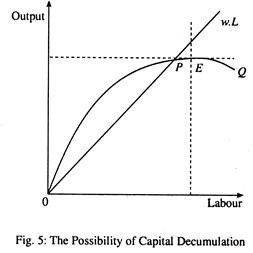
In this case E lies below the wage line. This means that maximisation of output will involve negative surplus. Point P gives maximum output consistent with the condition that the output covers the wage bill i.e., wL = Q. It is thus possible that maximisation of current output (and hence current consumption) may lead to contradiction through capital decumulation.
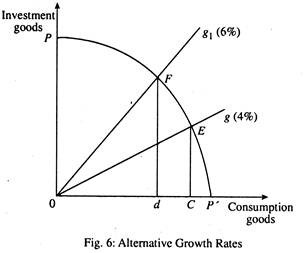
The moral e of the above exercise is to show clearly that there is basic conflict between maximising current consumption or maximising future consumption through higher investment. Let PP’ be the PPF form an LDC as shown in Fig. 6. If all the resources are allocated to the production of investment goods, OP of capital goods would be produced.
On the other hand, if all the resources are spent on the production consumer goods, OP’ of consumer goods would be produced. Obviously, the society would choose to produce some combination of both the goods. However, lines Og and Og1 represent different growth rates (say 4% and 6%) respectively. Let us assume that the economy is growing along Og.
But, if a higher growth rate (Og1) is regarded as desirable, it requires a reduction in consumption goods by wL, which would allow resources to be realised for the production of more investment goods to take the economy to F, given a rise in the production of investment goods, growth rate will be higher, i.e., 6% instead of 4%. But present consumption must be sacrificed to obtain the high growth path, though the choice of a higher growth path at present will ensure higher consumption, in the future as well.
As one of the solutions to the dilemma Amartya Sen had proposed that since the choice of technique comes to depend on the time-horizon of the output generation, the time-preference and the social welfare function the best way of looking at the problem would be to derive alternative time series of real income flow corresponding to each technique. Let us consider Fig. 7.
Let us consider an LDC having Hand L as two of its available options, where H is relatively capital intensive. Let us consider the growth rates r and r’ associated with L and H respectively. Then the time paths of consumption are exponentially given as
C (t) =A0.ert … (L)
C (t) = A 1.er’t … (H)
Let us first fix a time horizon and examine whether the loss of immediate output incurred by the more capital intensive technique is more than compensated by the extra output from it later before the period of consideration is over.
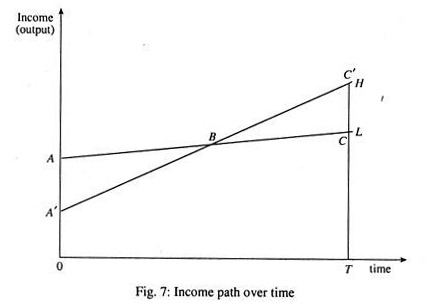
Let U denote the time horizon under consideration. We may actually consider a period of recovery (T) defined as the period of time in which the total output with the more capital intensive technique is just equal to that with the less intensive technique. Let the vertical axis measure the growth of output and the horizontal axis measure the time.
Output can be produced by either technique H or by technique L. Technique H produces less output now than technique L but after B the rate of growth of output of technique H is such as to compensate for the initial
loss of output by the year T. It is assumed that the area AA’B = BCC’. If U < T technique L is preferable and if U> T technique K should be chosen, the point of indifference being given by U = T. If we assume U= 1, the society is interested in maximisation of current output. If U= D, the society wants to achieve a higher rate of growth.
The defect of this approach lies in its arbitrariness. We have to assume that until the end of the period U, each unit of income is equally valuable and there is no preference over time. But beyond that point no income is of any value at all. This brings in the time factor rather suddenly and with extreme severity.
But such arbitrariness is difficult to avoid due to the very nature of the problem and the approach of the period of recovery may have considerable operational value. In any case by choosing the non-extreme values of it can be made less arbitrary than the approach of SMP criterion or that the criterion of reinvestment.
It is impossible to arrive at a realistic criterion for tackling this question which will be considered to be fully satisfactory intellectually. The objective of the exercise one has to remember is not perfection but minimisation of imperfection. The period of recovery approach can be properly understood only when this is recognised.
Some Observations on Relation between Wage Rate and Choice of Capital-Intensity:
Let us make certain observations on the relation between wage rate and the choice of capital intensity.
Firstly, it is important to remember that the production function is not continuous, so we cannot assume that as soon as the wage-rate falls by a little, we move over to a slightly less capital-intensive technique as no such technical alternative may be available. Thanks to such technological discontinuity, in the case of some industries the same technique may be preferred in widely different economies, a fact which has often been observed.
We have not yet ventured upon the problem of wage differentials. The wage rate may vary from technique to technique, depending upon productivity, skill and soon involve a higher wage level than the same industries in the rural area. In comparing the surplus rates of alternative techniques this consideration should be introduced. This point does not need much elaboration.
What may be somewhat more complicated is the probability of rise of wages over time. This not only affects the choice of techniques in the future, but also, in the case of durable plants, the choice of techniques is present.
When the pool of unemployed labour force is limited, this is an important factor to be borne in mind while choosing between techniques. Further, the rise in the level of real wages may not be independent of our decision about technology, because the speed of expansion of employment will vary from technique to technique. This possibility has also to be taken into account.
Finally, a few words on the role of wage rate as such: In a complete planned economy, the scope of direct manipulation of wage rate is also considerable. When the wage rate can be manipulated, the conflict (given a reserved army of labour) between the maximisation of immediate output and that of growth rate involved in technological choice disappears.
We choose the technique which maximises the level of immediate output given the investment and choose whatever saving rate we want by manipulating the wage rate. When the wage rate is completely under control, the level of employment need not have any influence on the rate of consumption.
Thus, there is no argument with these assumptions, from deviating from the maximisation of total output of consumer good given the investment in the field. In practice, however, even in a completely planned economy, the wage rate is never fully within our control. Governed by customs, trade unions pressures, immobility and incentives the wage rate is not entirely a policy variable.
The planning authority may, of course, exert some influence on the precise level of it but this is not strong enough to make the consumption creating effect of extra employment entirely irrelevant. And, therefore, the conflict between the maximisation of immediate output and that of the rate of growth is indeed not imaginary.
Conflict between Output and Employment:
In spite of relatively impressive rates of individual output growth in many LDCs, the rate of employment growth has lagged significantly behind. In a number of cases it has been stagnate. In what follows we will examine why rapid industrial output growth has failed to generate corresponding rapid rates of employment growths.
Basically the answer lie in the growth of labour productivity. By definition the rate of growth in output (0 minus the rate of growth in labour productivity (Q/L) approximately equals the rate of growth of employment (L) i.e.,
It follows that if labour productivity is growing at 8% while employment is growing by only 3%, the difference is due to the rise in labour productivity. The phenomenon of rising labour productivity associated with highest capital-labour ratio can be explained (at least theoretically better) with the aid of a variable proportions neoclassical model.
Recall that this model of savings, capital accumulation and economic development—the latter term defined simply as maximum output growth purports to demonstrate the higher capital-output ratios (i.e., more capital intensive production methods) will generate larger profit shares, higher savings ratios and, thus, higher rates of growth.
The optimal savings rate i.e., the one which leads to output growth can be generated only by relatively capital intensive methods of production. Maximum output and maximum employment growth are, therefore, seen as conflicting objectives.
In general, increases in labour productivity are desirable. But what is really desirable are increases in total factor productivity, output per unit of all resources. The productivity of labour can increase for a variety of reasons, some good and some not so good.
Improved education, better training and better management are all desirable reasons for increased productivity. But increases as results of substitution of capital for labour in production process or as a result of the importation of sophisticated and expensive labour saving machinery and equipment (e.g., tractors, powerfully automated textile machinery, heavy construction equipment) may be less satisfactory in heavily populated nations. Not only can such capital accumulation waste valuable domestic financial resources and foreign exchange, but it can also curtail the growth of new employment opportunities.
Moreover, the importation of inappropriate and expensive labour saving capital equipment may, in fact, reduce total factor productivity and thereby increase average costs of production even though average labour cost falls, the average total costs of production may rise because of the under-utilised productive capacity that often results when expensive mechanical equipment designed for large scale production in developed countries is imported into LDCs where the local market is too small for its efficient utilisation.
It is far from self-evident that higher levels of employment must necessarily be achieved at the expense of output growth. Just as there is widespread disagreement with the conventional wisdom of the 1950s and 1960s which assumed that income growth and more equitable distributions of income are mutually exclusive objectives, so too many economists have now come around to view that an employment-oriented (and, therefore, indirectly poverty-oriented, development strategy is also likely to be one which accelerates rather than retards overall economic progress.
This is especially true with regard to the growth and development of rural and small scale urban sector. More employment means more income to the poor which, in turn, implies a greater demand for locally produced basic consumption goods. Since these products tend to be more labour intensive than many of those produced by large scale industry, it follows that more jobs and higher incomes can become self-reinforcing phenomena.
They ultimately lead to high growth rates of both output and aggregate employment. But, in order to achieve this dual objective, a complementary policy of removing factor price distortions and promoting labour intensity technologies of production may be required.