The Classical Theory of Interest | Microeconomics

In this article we will learn about:- 1. Introduction to Interest 2. Stability of Equilibrium 3. Full Employment Equilibrium 4. Critical Evaluation of the Classical Theory.

Introduction to Interest:

The classical theory of interest rate determination says that people save and let their saving be loaned out to be used as capital for the purpose of investment, i.e., these people supply capital. On the other hand, there are some people who borrow money on behalf of their firms to be used as capital in their business, i.e., these people demand capital.

According to the classical theory, there is perfect competition in the capital market with a large number of people that supply savings or capital and a large number of people that demand capital. The rate of interest is determined in such a market through the interaction of demand for and supply of capital.

Supply of Savings (or Capital):

The classical theory says that the supply of savings comes from the households. By spend­ing less than their incomes, the households save, and because of their savings, a portion of the national product may be used for investment purposes.

The amount of savings to be supplied depends upon the degree of abstinence and waiting involved in the act of savings. Some classi­cal economists emphasised the role of time preference as a determinant of the supply of sav­ings.

According to the classical theory, interest is the reward for abstinence and waiting and for the preference in favour of future consumption. That is why the more the rate of interest, the more the people would abstain from present consumption and the more would be the supply of savings.

We may write, therefore,

s = s(r),s’ > 0                                         (17.1)

Here S = aggregate saving of the economy

and r = rate of interest

From (17.1) we obtain that S is an increasing function of r, i.e., as r increases or decreases, s also increases or decreases, respectively.

Demand for Savings (or Capital):

According to the classical theory, demand for savings or capital at any particular rate of inter­est (r), depends on the marginal productivity of capital. To obtain maximum profit, the firms demand or use, at any particular r, that amount of capital (savings) at which the value of marginal product of capital per period becomes equal to the marginal interest expenses per period.

Under the law of diminishing returns, the marginal product of capital diminishes as the firm uses more of this factor. That is why the firm may demand more of capital only when the rate of interest diminishes (to balance the fall in MP_K). We may write, therefore,

i = i(r), i’ < 0                                              (17.2)

Here i = investment demand for savings

and r = rate of interest.

From (17.2), we obtain that i is a decreasing function of r, i.e., as r increases or decreases, i decreases or increases, respectively.

The classical theory of interest states that the equilibrium rate of interest is one at which the supply of savings become equal to the investment demand for savings. Therefore, the third equation of this theory is

s(r) = i(r)                                                (17.3)

Determination of the Equilibrium Rate of interest:

If we solve eqn. (17.3) for r, we would obtain the equilibrium value of the rate of interest and if we put this value of r in eqns. (17.1) and (17.2), we would obtain the equilibrium values of s and i, which would be equal to each other (s = i) in equilibrium.

We may mention here that eqns. (17.1) and (17.2) are called the behavioural equations, respectively, of the savers and the investors, and eqn. (17.3) is called the equilibrium condition of the classical capital market.

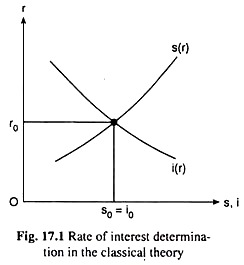
We shall now see how we may obtain the solution of the equation system (17.1)—(17.3) with the help of Fig. 17.1. In this figure, the s(r) curve is the supply curve of savings. This curve is the graph of the saving function (17.1).

Since s is an increasing function of r, the slope of the s(r) curve is positive. We may know from the s(r) curve what would be saving(s) of the economy at any particular rate of interest (r). Since the slope of the s(r) is positive, s would increase (diminish) as r increases (diminishes).

The i(r) curve, on the other hand, is the investment demand curve for savings. This curve is the graph of the investment function (17.2). Since i is a decreasing function of r, the slope of the i(r) curve is negative, i.e., i would diminish (increase) as r increases (diminishes). We may know from the i(r) curve what would be the investment demand for savings (i) at any particular rate of interest.

In Fig. 17.1, at r = r₀, the supply of savings and the investment demand for savings have become equal to each other. Therefore, here the equilibrium rate of interest has been r = r₀ and the equilibrium amounts of savings and investment have been s₀ = i₀.

Stability of Equilibrium:

We see in Fig. 17.1 that at r > r₀, we would have s > s₀ and i < i₀. As a result, here the supply of savings would be greater than demand for savings. Since there is perfect competition in the classical capital market, r in this case would be diminishing owing to competition among the savers over lending out their savings, till r comes down to its equilibrium level, r₀, and, conse­quently, the saving-investment equilibrium is restored.

On the other hand, at r < r₀, we would have s < s₀ and i > i₀. As a result, here the investment demand for savings would be greater than the supply of savings. Now, owing to competition among the investors over getting the supply of capital, r would be increasing in the market till r goes up to its equilibrium level, r₀, and, consequently, the saving-investment balance is restored.

We have seen in the above analysis that if the classical capital market is not in equilibrium, then the savers and/or investors behave in such a way that the equilibrium is (soon) restored in the market. That is why the equilibrium in the classical capital market is considered to be a stable equilibrium.

Conditions for Stability of Equilibrium:

Here we have two behavioural assumptions. First, if s > i, then owing to competition among the savers, r would fall. Second, if i > s, then owing to competition among the investors, r would rise. Now, stability of equilibrium in the capital market requires that subject to these two behavioural assumptions, s should be greater than i if r is greater than r₀, and i would be greater than s if r is less than r₀.

The significance of these conditions is not difficult to understand. If s > i at r > r₀, then owing to the first behavioural assumption, r would decline and so it would be possible for r to become equal to r₀ subsequently, and for the system to come back to equilib­rium.

Similarly, if i > s at r < r₀, then owing to the second behavioural assumption, r would increase and so it would be possible for r to become equal to r₀ subsequently, and it would be possible for the market to come back to equilibrium.

We have derived above the conditions for stability of equilibrium in the capital market. It is evident that these conditions would be satisfied if the s(r) curve is positively sloped and the i (r) curve is negatively sloped. That is why the equilibrium shown in Fig. 17.1 is a stable equilibrium.

Full Employment Equilibrium:

We have to note here that the saving-investment equilibrium in the classical capital market implies the demand-supply equilibrium in the goods market.

For, the saving-investment equi­librium implies that the value the savers save is equal to the value the investors invest, i.e., the goods and services (worth that value) that the savers would not purchase, would be purchased and used by the investors for investment purposes, which in its turn implies goods market equilibrium. In other words, eqn. (17.3) is the classical capital market equilibrium condition as well as the goods market equilibrium condition.

Now, the classical economists thought that there is perfect competition in the market for each good and service. Because of this, there would occur no problem of oversupply in the market for any good or service. For if, in any market, sellers are not able to sell what they are willing to sell, then the price would come down to make the necessary demand-supply adjust­ment.

Therefore, under perfect competition, there would be full utilisation and employment of the economy’s state of technology and resources, and, people’s willingness to work. As a result, the national production would be in equilibrium at the maximum possible level.

In these circumstances, if there is saving = investment equilibrium in the capital market implying de­mand = supply equilibrium in the goods market, then there would be no problem of deficient demand or excess demand in the latter market, and there would be no harm to full employment equilibrium in the economy.

Therefore, (subject to other assumptions), the existence of saving-investment equilibrium (17.3) in the capital market is also the condition for full employment equilibrium in classical macro-economy.

Critical Evaluation of the Classical Theory:

Economists have pointed out some defects of the classical theory of interest. These are:

(i) The classical economists thought that interest is a real phenomenon. For, according to them, the rate of interest depends on some real factors only.

(ii) It has been assumed in the classical theory that there is full employment in the economy. Therefore, if the producers increase capital goods production, then the output of consumer goods would have to decrease, i.e., the households would have to abstain from present con­sumption, i.e., the households would have to save some portion of their income—they cannot spend all their income on consumption.

As a reward for this, the households should get interest. So far the classical theory’s contention is correct. But if a situation of less than full employment prevails in the economy as it does in many countries, then the classical theory cannot explain why there should be interest.

For, if there are unemployed resources in the economy, then these may be utilised in the production of capital goods without hampering the production of con­sumer goods. The households in this case are not required to abstain from present consump­tion, and the question of giving them any reward in the form of interest does not arise.

(iii) Keynes has told us about another major defect of the classical theory. The classical theory assumes that saving (s) is a function of the rate of interest (r) [eqn (17.1)]. But, according to Keynes, although saving depends on the rate of interest, saving is more dependent on income.

If incomes of households and the income of the country in aggregate increase or decrease, then the savings of the households or the saving of the country in aggre­gate, also increase or decrease. Therefore, in place of (17.1), we should write

where s = aggregate saving of the economy, y = level of the economy’s income

and r = rate of interest.

Now, as Keynes has said, saving depends on the rate of interest as also on income, then, in order to know the position of the s(r) curve or function in Fig. 17.1, we have to know the level of income (y) of the country.

Again, in order to know y, we have to know the level of investment and in order to know i, we have to know the rate of interest (r), for i = i (r) [eqn (17.2)].

Therefore, Keynes has said that while going to determine r in classical theory, we have know r beforehand. In other words, according to Keynes, the classical interest theory is indeterminate—this theory cannot determine a unique interest rate.