Economies of Scale (With Diagram)

Economies which arise from the firm increasing its plant size. We will concentrate on the economies which may be achieved within a particular plant.

However, economies of scale may also arise from an increase in the number of plants of a firm, irrespective of whether the firm continues to produce the same product in the new plants or diversifies.

In general, such inter-plant economies of scale are of the same nature as the single-plant (intra-plant) economies, although the importance of each type of scale economies may be different with an increase of the scale of operations of the firm via the installation of additional plants.

It is important to stress once more that the scale economies determine the shape of the LRAC curve (the ‘scale curve’ as this is often called), while the position of this curve depends on external economies such as a change in technology (improvement in techniques) and changes of factor prices in the industry or the economy as a whole. Changes in these external economies will result in a shift of the LRAC.

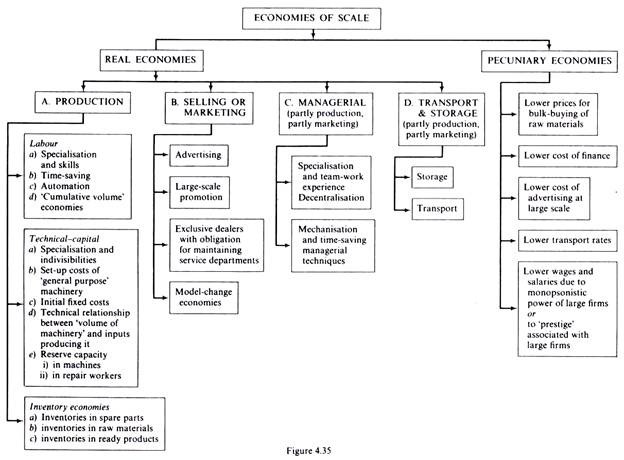
Firstly we will present the various types of economies of scale and their causes. Subsequently we will examine the possibility of negative economies (diseconomies) as the plant grows beyond a certain size. There are various possible classifications of economies of scale. We will adopt the classification which is shown schematically in figure 4.35.

Economies of scale are distinguished into real economies and strictly pecuniary economies of scale. Pecuniary economies are economies realized from paying lower prices for the factors used in the production and distribution of the product, due to bulk-buying by the firm as its size increases. Such strictly monetary economies do not imply an actual decrease in the quantity of inputs used but accrue to the firm from lower prices paid for raw materials (bought at a discount due to the large volume of the purchase), lower interest rates (and lower cost of finance in general) as the size of the firm increases, or lower wages and salaries.

Lower wages are rare and can result only if the firm becomes so large as to acquire the power of a labour monopolist or near-monopolist, as for example some mining companies, and provided that there are no strongly organised labour unions. Lower salaries (and sometimes lower wages) may be paid by larger firms if there is some ‘prestige’ associated with the employment by such firms. It is often observed that employees prefer to work for a larger firm whose name is known, even if they could earn more by working for a small unknown firm. Real economies are those associated with a reduction in the physical quantity of inputs, raw materials, various types of labour and various types of capital, (fixed or circulating capital).

We may distinguish the following main types of real economies:

(i) Production economies,

(ii) Selling or marketing economies,

(iii) Managerial economies,

(iv) Transport and storage economies.

Clearly the last two categories are partly pro­duction and partly selling costs. Their presentation in distinct groups facilitates their analysis.

A. real economies of scale

Production economies of scale:

Production economies may arise from the factor ‘labour’ (labour economies), from the factor fixed capital (technical economies), or from the inventory requirements of the firm (inventory economies or stochastic economies).

Labour economies:

Labour economies are achieved as the scale of output increases for several reasons:

(a) Specialization,

(b) Time-saving,

(c) Automation of the production process,

(d) Cumulative volume’ economies.

Larger scale allows division of labour and specialization of the labour force with the result of an improvement of the skills and hence of the productivity of the various types of labour. In a small plant a worker may be assigned three or four different jobs, while in a large plant these jobs are assigned to different workers. This division of labour is not profitable at small scales of output, because the skilled workers would stay un­employed part of the time.

Division of labour, apart from increasing the skills of the labour force, results in saving of the time usually lost in going from one type of work to another.

Finally, the division of labour promotes the invention of tools and machines which facilitate and supplement the workers. Such mechanization of the production methods in larger plants increases the labour productivity and leads to decreasing costs as the scale of output increases.

A classic example of the labour economies of large-scale production is the motor-car industry. Large-scale production made possible the introduction of the assembly-line, a process which involves a very wide specialization of the workers, each one of whom performs a single job to which he is assisted by special tools.

The assembly-line involves extensive investment in machinery and other equipment and its use is unprofitable for small-scale production. At large scales, however, this method of high automation resulted in huge increases in the productivity of labour and made possible the mass production of motor cars at low costs and prices. With increasing scale there is a ‘cumulative effect’ on the skills of technical personnel in particular. Production engineers, foremen and other production employees tend to acquire considerable experience from large-scale operations. This ‘cumulative-volume’ experience leads to higher productivity and hence to reduced costs at larger levels of output.

Technical economies:

Technical economies are associated with the ‘fixed capital’ which includes all types of machinery and other equipment.

The main technical economies arise from:

(a) Specialization and indivisibilities of capital,

(b) Set-up costs,

(c) Initial fixed costs,

(d) Technical volume/input relations,

(e) Reserve capacity requirements.

The main technical economies result from the specialization of the capital equipment (and the associated labour) which becomes possible only at large scales of production, and from the indivisibilities which are a characteristic of the modern industrial techniques of production. Modern technology usually involves a higher degree of mechanization for larger scales of output. That is, the production methods become more mechanized (capital intensive) as the scale increases.

Mechanization often implies more specialized capital equipment as well as more investment, a fact that makes the large-scale methods of production have high overhead costs. Of course these methods have lower variable costs, but at low levels of output the high average-fixed costs more than offset the lower labour (and other operating) costs. Once the appropriate scale is reached the highly mechanized and specialized techniques become profitable.

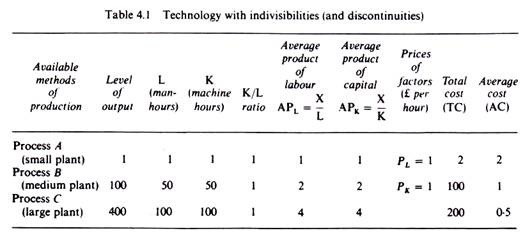
An example will illustrate how 0specialisation of the plant and technical indivisibilities results in economies of scale. Assume that there are three methods of producing a certain commodity, a small-scale method (Process A) suitable for producing at minimum cost ‘1 unit’ of output, a medium- scale method suitable for producing optimally (i.e., with minimum cost) 100 ‘units’ of output (Process B), and a large-scale method suitable for producing 400 ‘units’ of output (Process C). The first method uses 1 unit of labour and 1 unit of capital per unit of output.

The second method uses 50 units of labour and 50 units of capital, and the third uses 100 units of labour and 100 units of capital. Clearly the labour/capital ratio is the same in all three techniques, but the larger-scale techniques have a higher pro­ductivity (as measured by the output per man, X/L) due to the specialisation of labour (direct and managerial) which becomes possible only at the large scales of production.

The three techniques are indivisible, that is, the technology is characterised by in­divisibilities in the sense that each size plant can be duplicated but cannot be halved and retain its higher productivity. Furthermore, all techniques are assumed to have constant returns to scale. The above technology is summarised in table 4.1.

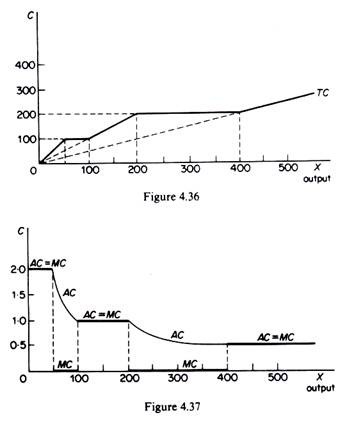
Let us look at the shapes of the AC and the MC when indivisibilities are present in the technology of a firm. Increasing technical returns to scale (with constant factor prices) in the long run are explained by indivisibilities. It is because the firm cannot continue to reduce all inputs proportionately when output is reduced that long-run average cost is bound to rise with reduction in output. Or, to put it in another way, large-scale plants cannot be halved (or decreased in another ratio) and still remain equally efficient. Assume constant prices of factors, £1 per man hour and £1 per machine hour. The total and average cost for each process are shown in the last two columns of table 4.1 and are plotted in figures 4.36 and 4.37.

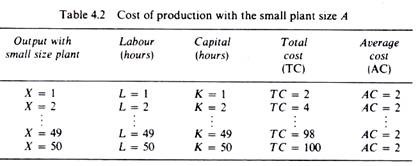
For each level of output the least-cost process will be chosen. Up to X – 49 the small-scale process is the one with the least cost (equal to £2 per unit of output). At X = 49 the firm uses 49 man hours and 49 machine hours. The total cost increases proportionally with output, as can be seen from table 4.2.

The level of output X = 50, if produced with the small-scale process, would cost £100 (50 labour cost + 50 machine cost). However, with the same cost (i.e. by employing the same quantities of factors, 50L and 50K) the firm can produce 100 units of output by adopting the second method of production, thus reducing its average cost to £1 (per unit of output).

At any level of output higher than 50 units process B has a lower cost than process A, and hence for X > 50 the firm will switch to process B. For any level of output 50 < X < 100 total cost will be constant (equal to £100) ir­respective of the level of production within these limits, because with 50L and 50K the firm can produce any output up to 100 units. Clearly the AC would fall continuously over the range of output 50 to 100, since total cost remains constant at the level of £100. Beyond the level of X – 100 total costs will start rising, since more L and more K will be required. However, AC will remain constant at £1 per unit of output (see table 4.3).

The level of output X = 200, if produced by process B, would cost £200 and would require 100L and 100K. However, with the same quantities of factors (and presumably the same total cost) the firm could produce 400 units of output by switching to process C. At any level of output higher than 200 units, process C has a lower cost than either of the other processes. Hence it will be chosen by the rational producer.

For any level of output 200 < X < 400 total cost will be constant (equal to £200), with AC falling con­tinuously over this range. Beyond the level of 400 units of output total cost would start rising proportionally with output, since more L and K would be required (for X > 400, L > 100 and K > 100). However, the AC will remain constant (at £0-5 for levels of X greater than 400 units).

The MC would be equal to the AC over the flat parts of this curve, but would be zero over the falling parts of the AC curve. This is because over these ranges of X (for which AC is falling), total cost remains constant, and hence MC = 0.

The AC and MC curves in the case of technological indivisibilities are shown in figures 4.36 and 4.37. Set-up costs are the costs involved in the preparation (arrangement) of ‘multi­purpose’ machinery for performing a particular job or product. For example in the motor-car industry or in firms producing electrical household equipment the use of ‘general-purpose’ machines is quite common. One such type of machinery is the metal- stamping press which produces the frames and various components of the final product.

The metal stamping press has to be reset any time that a particular part of, say, a car has to be produced. For example, different set-ups are required for producing the doors, the roof, the wings of a car, and each set-up involves considerable time and cost. The larger the scale of output the more a multipurpose machine is left to one set-up (say, stamping doors) and hence resetting becomes less frequent. This is a source of technical economies of large-scale production.

‘Initial costs’ are usually involved in starting a business or introducing a new product. Research and development expenditures, costs of market exploration, design costs for the product are examples of such costs. Clearly the larger the scale of output, the lower the unit costs of such ‘fixed’ expenses.

Technical economies of scale also arise from some technical-geometric relationships between particular equipment and the inputs required to produce and install it. These are important in the so-called ‘process industries’, such as petroleum refining, steam generation, gas transmission, chemical industry, cement industry, glass manufacturing, and iron reduction.

The methods of production used in the ‘process-industries’, includes special equipment, such as storage tanks, reaction chambers, connecting pipes, etc. The material and labour costs of constructing such plants are proportional to the surface area that they occupy. But the volume capacity (which determines the level of output) of a plant increases more than proportionately as the area increases.

Hence the technical cost of installing such industrial plants falls as the output (volume) capacity increases, at least up to the point where the equipment becomes so large as to require stronger materials and special constructions in order to make the larger plants safe.

Another source of technical economies are the so-called ‘reserve-capacity’ economies. Firms always want some reserve capacity in order to avoid disruption of their production flow when breakdown of machinery occurs. A small firm which uses a single large machine will have to keep two such machines if it wants to avoid disruptions from a breakdown.

A larger firm which uses several large machines can attain the required ‘security’ from breakdowns by holding only a proportion of their total numbers as reserve capacity. Similarly the number of workers required for repairs within the firm does not increase proportionately with the size of scale.

Inventory economies:

These are sometimes called ‘stochastic economies’, because the role of inventories is to meet the random changes in the input and the output sides of the operations of the firm. Stocks of raw materials do increase with scale but not proportionately. Random fluctuations in the supply of such inputs are smoothed out with stocks whose size needs change by less than the size of the firm.

The ‘reserve-capacity’ economies discussed in the previous paragraph are also a type of stochastic economies. The breakdowns in machinery do not increase pari-passu with size. If anything the ‘cumulative volume’ experience of production personnel will tend to reduce the frequency of such breakdowns in larger plants, and require a pro­portionately smaller amount of reserve machinery and stocks of spare parts.

Similarly on the demand side, random changes in the demand of customers will tend to be smoothed out as the plant size increases. The larger the numbers of customers the more the random fluctuations of their demands tend to offset peaks and recessions, thus allowing the firm to hold a smaller percentage of its output to meet such random changes.

Selling or marketing economies:

Selling economies are associated with the distribution of the product of a firm.

The main types of such economies are:

(a) Advertising economies,

(b) Other large-scale econo­mies,

(c) Economies from special arrangements with exclusive dealers (representatives, or distributors, wholesalers or retailers),

(d) Model-change economies.

Advertising expenses are not necessary only for a new firm or a new product, but also for established firms, who need a minimum of advertising in order to keep their name in the minds of actual or potential customers. It is generally agreed that advertising economies do exist at least up to a certain scale of output.

Advertising space (in news­papers or magazines) and time (on television or radio) increase less than proportionately with scale, so that advertising costs per unit of output fall with scale. The advertising budget is usually decided on the basis of available funds, profits, similar activities of competitors, rather than on the basis of the output. Thus the larger the output the smaller the advertising cost per unit.

Similar considerations hold for other types of selling activities, such as the salesmen force, the distribution of samples, etc. Such large-scale promotion expenditures increase by less than proportionately with output, at least up to a certain scale.

Large firms can enter exclusive agreements with distributors, who undertake the obli­gation of maintaining a good service department for the product of the manufacturer. This is usual for the motor-car industry, where the dealers build up garages and keep regular stocks of spare parts for various models. The buyers of durables pay a lot of attention to the availability of spares and of good servicing-shops for the brands they buy.

In modern industry, firms need to change the style of their product quite frequently in order to meet the demands of their customers and the competition of the rival firms. A change in the model or style of the product often involves considerable expenses in research and development, and possibly on new materials and equipment. The spreading of such overheads is lower per unit if the scale of output is large.

Selling activities in general absorb productive resources. There is no general agree­ment among economists regarding the implications of advertising and other selling activities. Some economists argue that advertising is a waste of resources, since they do not add anything to the already-produced commodity, whose price to the consumer will, as a consequence, be higher.

Others argue that advertising is not a waste of resources, but a cost which consumers are willing to pay (in the higher price they are charged) in order to have a wider choice of products. Product differentiation is some­thing that consumers want, hence the selling costs associated with this differentiation are increasing the welfare of the consumers.

This argument implicitly assumes that all advertising and other selling activities are truly informative: they provide information to the buyers about the existence and the technical characteristics of the different varieties of a certain product. Whether this is true or not, and the extent to which selling activities are simply manipulative of consumers’ tastes, and create fancied differentiation for products technically identical (or almost identical) is a theme highly disputed in economic circles.

At this point we are interested not in the nature and the social justification of advertising and other selling activities, but in whether there are ‘economies of large-scale promotion’, that is, whether the selling cost per unit of output declines with the scale of the plant (or firm). It is generally agreed that such large-scale marketing economies do exist, at least up to a certain size of the plant (or firm).

Dis­agreement exists as to whether the average-selling-cost curve turns upwards at very large scales of output (due to diseconomies of selling activities) or whether the unit selling costs fall continuously with scale. Chamberlin argues on the lines of a U-shaped selling-cost curve while Andrews and others support the idea of a continuously-falling selling-cost curve. Given that the technical costs of production fall with scale, the total average-cost curve may eventually turn upwards if selling diseconomies do exist after a certain plant size. Empirical evidence is not conclusive in this respect.

Managerial economies:

Managerial costs are partly production costs and partly selling costs, since the managerial team in a firm is concerned with both the production and the distribution activities of the firm. The grouping of managerial costs in a separate category facilitates their analysis and in particular the analysis of possible sources of diseconomies of large- scale plants (see below).

Managerial economies arise for various reasons, the most important being:

(a) Specialization of management, and

(b) Mechanization of managerial functions.

Large firms make possible the division of managerial tasks. The existence of a pro­duction manager and a sales manager, a finance manager, a personnel manager and so on, is common in large firms, while all or most managerial decisions are taken by a single manager (who possibly is also the owner) in a small firm. This division of mana­gerial work increases the experience of managers in their own areas of responsibility and leads to the more efficient working of the firm.

Furthermore the decentralization of decision-making in large firms has been found very effective in the increase of the efficiency of management. With decentralization the flow of information within the firm is reduced and thus distortions and delays of this information in the various sections of the firm is to a large extent avoided. Decentralization of the decision-making process is one of the main means of increasing the efficiency of management in large scale plants and of avoiding managerial diseconomies in still larger plants.

Large firms apply techniques of management involving a high degree of mechanization, such as telephones, telex machines, television screens and computers. These tech­niques save time in the decision-making process and speed up the processing of informa­tion, as well as increasing its amount and its accuracy.

A problem still disputed in economic theory is whether managerial costs continue to decline at very large scales of output. In the traditional theory of costs, managerial diseconomies were assumed to be the cause of the upward turning of the long-run average-cost curve beyond a certain scale of output. Management, like any other factor of production, is variable in the long run.

However, traditional theory postulated that beyond a certain stage increases in management lead to less than proportionate increases in output and thus cause an increase in the long-run unit costs. The decrease in the efficiency of management is usually attributed to two factors. Firstly, loss of control of the top management once the firm has surpassed an optimum size. Decisions are delayed in the bureaucracy of large-size firms, where information is often con­sciously or unconsciously distorted as it passes through the various hierarchical levels, or is stopped for various reasons at some stage.

Obviously decisions of the top manage­ment will not be optimal if the information on which they are based is inaccurate or comes with time lags, during which crucial changes in the environment of the firm may have taken place. Secondly, the uncertainty (from the market conditions and the reac­tions of competitors) increases with size and this leads to eventually less efficient decision-making.

These arguments are attacked by other theorists, who argue that managerial diseconomies are not a necessary consequence of the increase in the scale of the plant. The decentralization of the decision-making process, the mechanization of various managerial tasks, the improvements in budgeting of the activities of the various depart­ments, the system of regular reports at the different levels of the administrative hierarchy, the use of computers and similar devices for the quick access and processing of informa­tion tend to offset the deficiencies of complex organisations, so that managerial dis­economies are not a problem in the modern industrial world.

Other writers argue that at very large scales of output the efficiency of management is somewhat adversely affected by the unavoidable complexity of big organisations, but the increase in costs from the managerial diseconomies is only slight at very large scales of output. And in general such diseconomies are more than offset by the technical- production economies, so that the total long-run average cost curve does not turn upwards at very large scales, but rather has the form of an ‘inverse J’.

Returning to the uncertainty problem, there is no general consensus among econo­mists that uncertainty increases with size and leads to eventually increasing costs. It is true that if the firm expands its share continuously in one market only the uncertainty from changes in market conditions increases (for example, a minor change in the market demand will greatly affect the sales of a dominant firm), but the uncertainty from the competitors will tend to be reduced since their share shrinks, and consequently their power will normally be weakened.

The balance between these opposite developments cannot be determined on strictly theoretical a priori grounds. If one considers the more realistic situation of firms diversifying in various markets, the above arguments are reversed: the market uncertainty is generally reduced for the multiproduct firm by the simple fact that it ‘does not put all its eggs in one basket’. On the other hand, the un­certainty from the reaction of competitors may well increase as the firm diversifies, since in this process the firm must anticipate the attitudes of the firms in the new markets in which it enters as well as its rivals in its old markets.

In summary, the controversy among theorists regarding the shape of managerial costs is not as yet settled. The empirical evidence from various studies of costs, shows that the total LAC curve is L-shaped, but since these studies include all types of costs, their evidence cannot be interpreted as refuting the U-shaped form of the managerial costs alone.

Transport and storage costs:

Transport costs are incurred partly on the production side (transportation of raw materials or intermediate products) and partly on the selling side of the firm (transporta­tion of final product to its markets). The same holds for storage costs. Storage costs will clearly fall with size. The construction of storehouses follows broadly the same rules of geometrical relationships between surface, capacity-volume and inputs. The storage-cost curve will thus be falling in general but will be scalloped, due to technical indivisibilities and discontinuities.

The storing capacity can normally be increased by increasing the number of floors of store­houses, in which case the geometrical input-output relationships clearly do hold. Beyond a certain scale additional storehouses will be required, the construction of which will increase the total cost, but unit costs will normally be lower the larger the output. The analysis of transport costs is more complicated. The exhaustive examination of transport costs goes beyond the scope of this book. We can, however, give some idea of the problems involved in the treatment of transport costs.

If the firm uses its own transport means (e.g., lorries) transport unit costs would fall up to the point of their full capacity. At larger scales of output it might be possible to use larger vehicles, in which case the unit costs would fall, and the LAC of transport would be falling and would have a scalloped form. Beyond the level of output which allows the employment of the largest available means of transport one should normally expect constant unit transport costs by duplicating, etc., of these means as output expands. If the firm uses public transport the unit costs would normally increase with distance. If special freight rates are obtained for larger quantities transported such pecuniary economies might offset the increases from the greater distance.

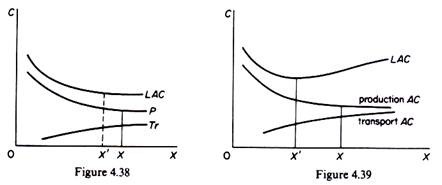
To the above considerations one should add three relevant aspects of transport: the distance to which the product has to be carried, the importance of transport costs relative to the value of the product, and the possibility of passing the higher transport costs to the buyer. If the transport costs are negligible relative to the value of the product and if the firm can pass the transport costs to the buyers, the average transport cost will be U-shaped, but will rise slowly with size, so that the effect of the transport costs on the optimal plant size will be negligible.

Such a case is shown in figure 4.38. Without taking into account the transport costs the minimum optimal scale of output is X, while the addition of transport costs (TrAC), which increase smoothly according to our assumptions, reduce the minimum optimal scale slightly, to X’. However, if the transport costs rise fast with distance and their amount is an important component of the total unit costs (without the firm being able to pass the increases to the buyers), the average unit trans­port costs will rise rapidly, offsetting possibly other economies of scale and reducing significantly the minimum optimal scale of plant. Such a situation is shown in figure 4.39.

B. pecuniary economies of scale:

These are economies accruing to the firm due to discounts that it can obtain due to its large scale operations.

The larger firm may achieve:

(a) Lower prices of its raw materials, bought at special discounts from its suppliers.

(b) Lower cost of external finance. Banks usually offer loans to large corporations at a lower rate of interest and other favourable terms.

(c) Lower advertising prices may be granted to larger firms if they advertise at large scales.

(d) Transport rates are often lower if the amounts of commodities transported are large.

(e) Finally, larger firms may be able to pay lower earnings to their workers if they attain a size which gives them monopsonistic power (for example, extraction industries in some areas), or due to the prestige associated with the employment by a large, well- known firm.

The total average cost is the summation of all costs (of production, marketing, managerial, transport, etc.). It is generally accepted that the total LAC curve falls as the scale of the plant (and of the firm) increases, at least up to a certain plant (or firm) size.

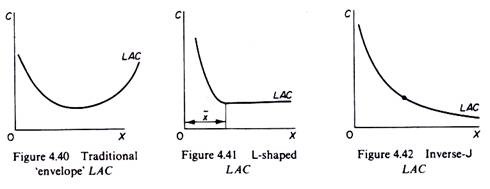
Disagreement exists among economists as to whether:

(a) There are diseconomies at very large scales of output (figure 4.40);

(b) There is a minimum optimum scale of output at which all possible economies have been reaped so that costs remain constant beyond that level (figure 4.41);

(c) There are economies of scale at all levels of output, although their magnitude becomes small beyond a certain scale (‘inverse J’ costs, figure 4.42).

Supports the view that there are no diseconomies of scale at large scales of output. The empirical evidence has not, however, established conclusively whether costs remain constant beyond a certain minimum optimum scale, or fall continuously with scale.