In this article we will discuss about the formula for calculating the arc elasticity of demand.
Elasticity of demand that is obtained at a point on the demand curve for a good as a consequence of an infinitesimally small change in its price, is called the point-(price-) elasticity of demand for the good.
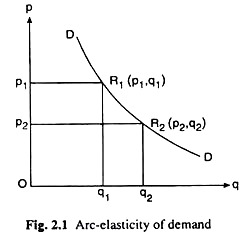
But if the change in price is not infinitesimally small, if the change is by a considerable amount, then move to another point on the demand curve which is somewhat away from the initial point. In this case, the elasticity of demand that is obtained over the arc of the demand curve between the two points is called the arc-elasticity of demand. This elasticity can be explained with the help of Fig. 2.1.
In Fig. 2.1, DD is the demand curve for the good. R1 (p1, q1) and R2 (p2, q2) are any two p points on DD. Initially, at the point R1, when the price is p1, demand is q1.
ADVERTISEMENTS:
Now if the price decreases by a considerable amount from p1 to p2, the demand for the good increases from q1to q2 at the point R2. The elasticity of demand that is obtained in the case of this price change is called the arc-elasticity of demand—here over the arc R1R2 of the demand curve.
It should be remembered here that if our initial point is R2 (p2, q2) and if, after a rise in price from p2 to p1, come to the point R1 (p1, q1), then the arc-elasticity of demand—now over the arc R2R1 is obtained. Since the two arcs, viz., R1R2 and R2R1, over the demand curve are identical, the arc-elasticities in these two cases would also be the same.
That is why, while measuring the arc-elasticity of demand over the arc R1R2 or R2R1, accept the average of p1 and p2, i.e., (p1 + p2)/2, as the initial price, and the average of q1 and q2, i.e., (p1 + p2)/2, as the initial demand.
ADVERTISEMENTS:
Therefore, the coefficient of arc-elasticity of demand over the arc R1R2 or R2R1would be: