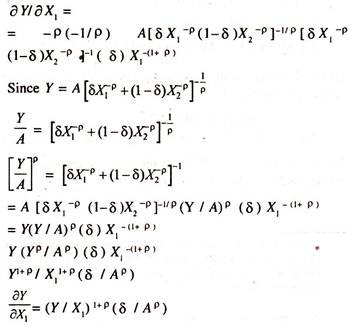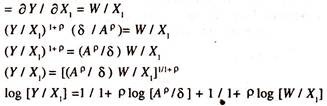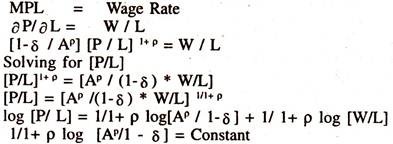In this article we will discuss about the constant elasticity of substitution production function.
Elasticity of Substitution:
One of the limitations of Cobb-Douglas production function is the unitary elasticity of substitution between labour and capital. This is a rigid assumption of Cobb-Douglas production function. “The elasticity of substitution in the Cobb-Donglas Production Function is unity” can be proved below.
The Cobb-Douglas production function:
Y = b0X1b1X2b2 ………………. (100)
ADVERTISEMENTS:
Where
Y = Production
X1 = Labour
X2 = Capital
ADVERTISEMENTS:
Marginal product of labour [∂Y/∂X1] is b1Y/X1 and
marginal product of capital [∂Y/∂X2] is b2Y/X2.
The ratio of marginal product of capital to marginal product of labour is known as marginal rate of technical substitution [MRTS] i.e.,
MRTS = MPX2/MPX1
ADVERTISEMENTS:
= b2Y/X2 /b1Y/X1 = b1Y/X2.X1b1Y = b2X1 /b1X2
The estimate of elasticity of substitution between two inputs [Labour and Capital] will be obtained by regressing log [X1/X2] on log [MRTS] or log [b2X1/b1X2]
The derivative of log X1/X2 with respect to log b2X1/b1X2 is b1, which will always be unity. Therefore there is a need to follow other production function. One such type of production function is the CES [Constant Elasticity of Substitution] production function.
This production function will be specified as follows:
ADVERTISEMENTS:
Where
Y = Production
X1 and X2 = Labour and Capital inputs respectively.
ADVERTISEMENTS:
A = Efficiency parameter > 0
δ = Distribution parameter 0 < δ < 1
ρ = Extent of substitution between labour and capital related to σ = 1/1+ ρ;
σ = Elasticity of substitution
ADVERTISEMENTS:
As there is no method of linearization by a simple logarithmic transformation, the research investigators attempt to estimate the CES Production Function by marginal productivity conditions.
From the above function, the marginal productivity of labour will be obtained as follows:
ADVERTISEMENTS:
ADVERTISEMENTS:
ADVERTISEMENTS:
The marginal productivity theory of wages will generally be accepted on the grounds that it gives an adequate explanation for wage determination. It is well known that the price of labour [wage] under the conditions of perfect competition is equal to average and marginal product of labour in the long-run.
The firm being a profit maximizer will continue to increase the labour force until the marginal unit of labour [marginal wage] is equal to the contribution made by the labour unit [marginal productivity of labour]. According to marginal productivity theory under perfect competition [Most Ideal Situation ie., Absence of Exploitation]
MPX1= Real Wage rate [nominal wage rate/consumer price index]
ADVERTISEMENTS:
1/1 + p = σ = constant elasticity of substitution or elasticity of labour productivity.
Y/X1 = constant* [W/X1]σ
log [Y/X1] = constant + σ log [W/X1] …………..(103)
The coefficient of log W/X1 in the above regression of log Y/X1 on W/X1 yields an estimate of σ.
The possible values of ρ range from infinity to -1, when ρ = 0, σ = 1 leads to a Cobb-Douglas production function. More specifically from the partial elasticity of labour productivity it can be inferred that if σ more than 1, then there will be higher substitution possibilities and if σ is less than one, then there will be lower substitution possibilities. The estimation form of the above equation is log Y/X1= Constant + σ log W/X1.
The above equation will be estimated underlying the assumption of constant returns to scale. The numerical value of a may not be unity as in the case of Cobb-Douglas can take any value which will ‘be different from unity. If the numerical value of σ is unity, then we have Cobb-Douglas production function.
On the basis of the value of a, the form of production function [Cobb-Douglas or Constant Elasticity (CES) Production function] can be selected for the analysis. In most empirical studies relating to either industry or agriculture, the CES production function is used to know the extent of substitution possibilities between labour and capital.
If the elasticity of substitution estimated from the CES production function is more than unity, then it can be inferred that the substitution possibilities will be more in favour of the labour input. If it is less than unity, then there will be low substitution possibilities in favour of labour input.
It should however be noted that the estimation of the above function by OLS method is subjected to one way causation showing that labour productivity depends on real wage rate only. The variable real wage will be obtained by deflating the nominal wage rate [Wages/Labour] by the consumer’s price index.
Sometimes the wage rate at constant prices [Real wage] will also be considered. In empirical studies in the field of agriculture, the cross-section data [at a point of time] will be considered to examine the substitution possibilities between labour and capital or between two inputs across the farms belonging to different holdings.
In the case of industries, the time-series data [over a period of time] will be considered to examine the substitution possibilities between labour and capital. In the case of cross section data, the problem of heteroscadacity and in the case of time-series data, the problem of auto-correlation would creep. The problem of autocorrelation can be reduced by adopting the first difference method.
If two way causation [i.e., the wage rate will be an endogenous variable] is present then the application of OLS method breaks down. Then the estimation of the CES Production Function has to be estimated by either indirect least squares method [ILSM] or two-stage least squares method [TSLSM]. By applying these methods, the simultaneous bias in the estimate of coefficient of elasticity of substitution[σ] can to some extent be reduced.
CES Production Function:
Estimates of Elasticity of Substitution:
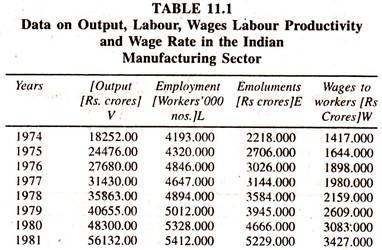
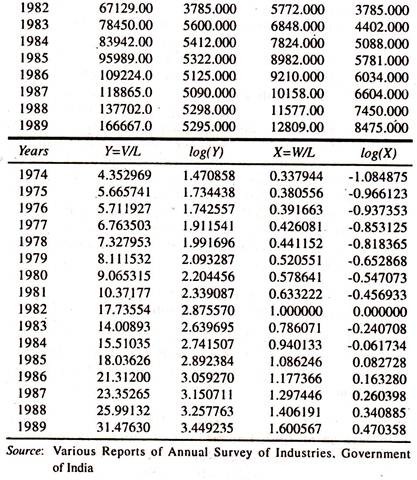
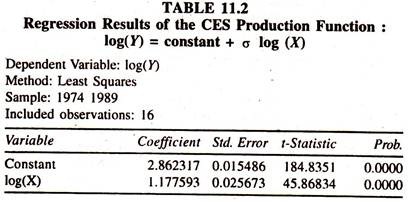
The following data [Table 11.1] are considered for estimating the CES Production Function. The Regression Results [Table 11.2] show the nature of CES Production Function.
The regression results of the CES production function [Table 11.2] show that the regression coefficient of the log wage rate, log(W/L) , which is constant elasticity of substitution, is significantly different from unity confirming that the choice of the CES production function is correct.
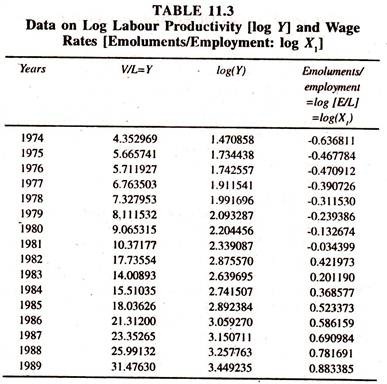
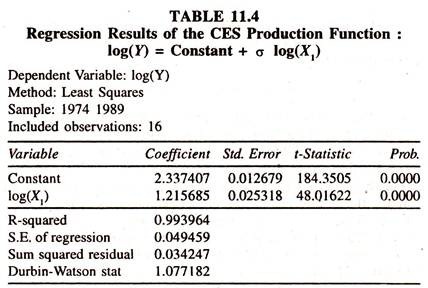
When the new variable [emoluments/employment log (E/L) = logX1 [Table 11.3] is considered, the regression coefficient of log X1[Table 1 1.4] is also found to be significantly different from unity confirming that the choice of the CES production function is correct.
Variable Elasticity of Substitution [VES] Production Function:
In order to provide empirical content to elasticity of substitution between the inputs [labour and capital] separately, the following constant elasticity of substitution [CES] production function will be fitted to the cross section/ time series data. The specification of the CES production function on the assumption that it is independent of the changes in capital-labour ratio [capital intensity] is
P = A [δ K-ρ +(1- δ) L-ρ] -1/ ρ
Where
P = Production
K and L = Capital and Labour inputs respectively.
A = Efficiency parameter
δ = Extent of substitution between labour and capital related to σ = 1/ 1+ ρ
The above equation can be estimated empirically by OLS method under the marginal productivity conditions, [marginal productivity of labour = wage rate].
The marginal productivity of labour [Employment] can be obtained from the above function as follows:
Equilibrium condition between ∂ P/∂ L and W/L [i.e., Marginal Product of labour [MPL] is equal to Wage Rate], the most ideal situation that represents the absence of exploitation of the labour, is
1/1+ p = σ = Elasticity of Substitution or Elasticity of labour productivity with respect to wage rate.
log [P/L] = Constant + σ log [W/L]
The coefficient on log W/L in the above regression of log P/L on log W/L is the estimate of constant elasticity of substitution between labour and capital, σ.
σ = 1/1+ ρ
ρ = (1 / σ)-1
log [P/L] = Constant + σ log [ W/L]
The above equation will be estimated under the constant returns to scale [Linear Homogeneous Production Function] and equilibrium [marginal product of labour = wage rate] conditions. The numerical value of σ need not be unity as in the case of Cobb-Douglas and can take any value, which is different from unity. If the numerical value of σ is unity, then we have a Cobb-Douglas production function.
Depending on the value of σ, the form of production function [Cobb-Douglas or CES Production function] would be selected for analysis. The CES production function is used to know the extent of substitution possibilities between labour and capital. If the elasticity of substitution estimated from the CES production function is more than unity, then it can be inferred that the substitution possibilities are more in favour of labour input.
If it is less than unity, then there will be low substitution possibilities in favour of labour input. It should however be noted that the estimation of the above function by OLS method is subjected to one way causation showing that labour productivity depends on wage rate only.
The above function is independent of changes in the capital – labour ratio. Its known fact that the input combinations [K/L] go on changing due to input prices [factor price ratio] owing to which the elasticity of substitution varies. In order to see whether the function is independent of changes in input combinations , the ratio of capital to labour , K/L , is included as the independent variable along with wage rate in the CES function.
Then the specification of the model, known as VES production function which explicates that labour productivity [P/L] is a function of wage rate [W/L] and capital- labour ratio [K/L], will be as follows:
log [P/L] = Constant + σ log [W/L] + β log [K/L]
Where
∂ log [P/ L] /∂ log [W/L] = σ [Elasticity of labour productivity with respect to wage rate]
∂ log [P/ L] /∂ log [K/L] = β [Elasticity of labour productivity with respect to capital intensity]
If the regression coefficient of K/L, β, is not significant then the elasticity of substitution will be constant though not unity.i.e., CES function will be independent of capital-labour [capital intensity] ratio.
If β is significant then there will be strong evidence of argument to retain capital – labour ratio along with wage rate for explaining the variations in the average productivity of labour. In other words the value of elasticity of substitution may vary with the change in capital labour ratio.i.e.,CES function will be not independent of the changes in capital-labour ratio.