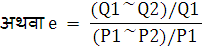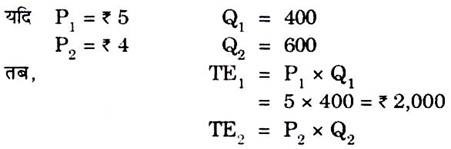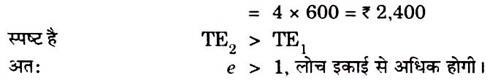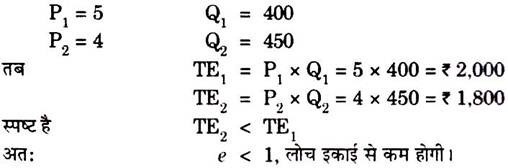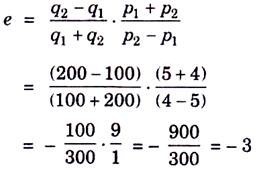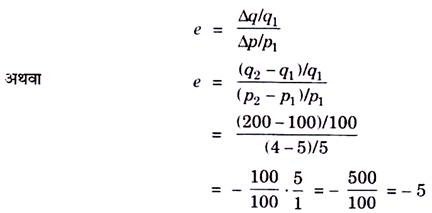Measuring Elasticity of Demand | Hindi | Economics

Read this article in Hindi to learn about the four main methods used for measuring the elasticity of demand for a commodity.

1. प्रतिशत या आनुपातिक रीति (Percentage or Proportional Method):

इस रीति का प्रतिपादन प्रो. फ्लक्स (Flux) ने किया था । अतः इस रीति को फ्लक्स की रीति भी कहते हैं ।

इस रीति के अनुसार,

.

जहाँ:

P₁ = पूर्व कीमत,

Q₁ = पूर्व माँग,

P₂ = नवीन कीमत,

Q₂ = नवीन माँग

(चिह्न ͠ दो संध्याओं के बीच का अन्तर निकालने के लिए प्रयुक्त होता है तथा इसमें ऋणात्मक तथा धनात्मक दोनों दशाओं में फल को धनात्मक ही माना जाता ।)

किन्तु माँग की लोच की उपर्युक्त माप त्रुटिपूर्ण है । माँग की लोच का सही मूल्यांकन करने के लिए यह आवश्यक है कि माँग और कीमत के आनुपातिक परिवर्तन को ज्ञात करने के लिए औसत (Average) की सहायता ली जाए ।

अतः फ्लक्स के संशोधित समीकरण में माँग का आनुपातिक परिवर्तन न तो आरम्भिक माँग पर निकाला जाता है और न ही परिवर्तित माँग पर, बल्कि इन दोनों मात्राओं के मध्य-बिन्दु पर निकाला जाता है । यही विधि कीमत के आनुपातिक परिवर्तन की गणना में भी अपनायी जाती है ।

उदाहरण द्वारा स्पष्टीकरण:

अर्थात् माँग की लोच इकाई से कम है ।

2. कुल आगम अथवा व्यय रीति (Total Outlay or Expenditure Method):

यह रीति मार्शल द्वारा प्रतिपादित की गई है । मार्शल के अनुसार माँग वक्र पर वस्तु की माँग में विस्तार अथवा संकुचन उसकी कीमत के परिवर्तन के सापेक्ष होता है परन्तु यह आवश्यक नहीं कि यह परिवर्तन कीमत के अनुपात में ही हो । एक ही माँग वक्र पर कीमत के परिवर्तन के सापेक्ष वस्तु की माँग में कितना परिवर्तन होगा, यही माँग की लोच की माप है ।

कीमत में परिवर्तन के सापेक्ष माँग में परिवर्तन का अर्थ है उपभोक्ता के कुल व्यय में परिवर्तन । दूसरे शब्दों में, हम कह सकते हैं कि माँग की लोच उपभोक्ता के कुल व्यय परिवर्तन की माप है ।

कुल व्यय = कुल आगम

= वस्तु की कीमत x वस्तु की माँग

अर्थात् कुल व्यय से अभिप्राय उस कुल राशि से होता है जो वस्तु की कीमत को वस्तु की कम की गई इकाइयों के गुणा करने से प्राप्त होती है ।

इस रीति द्वारा माँग की लोच के अंश तीन प्रकार के होते हैं:

(a) इकाई के बराबर माँग लोच (Equal to Unit Elasticity):

यदि कीमत में वृद्धि या कमी होने पर भी कुल व्यय स्थिर रहता है तब माँग की लोच इकाई के बराबर होती है । दूसरे शब्दों में, कीमत परिवर्तन के बाद एवं कीमत परिवर्तन से पूर्व की दोनों व्यय राशियाँ यदि एक समान होती हैं तब माँग की लोच इकाई के बराबर होती है ।

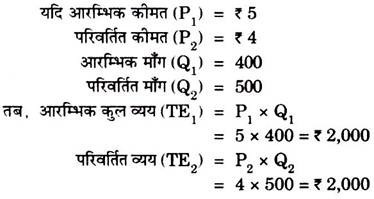
(b) इकाई से अधिक माँग लोच (Greater than Unit Elasticity):

कीमत के घटने पर कुल व्यय बढ़ता है अथवा कीमत के बढ़ने पर कुल व्यय घटता है तब माँग की लोच इकाई से अधिक होगी । दूसरे शब्दों में, जब कीमत परिवर्तन एवं कुल व्यय परिवर्तन विपरीत दिशा में चलते हैं तब माँग की लोच इकाई से अधिक होती है ।

(c) इकाई से कम माँग लोच (Less than Unit Elasticity):

यदि कीमत के घटने पर कुल व्यय घटता है अथवा कीमत के बढ़ने पर कुल व्यय बढ़ता है तब माँग की लोच इकाई से कम होती है । दूसरे शब्दों में, जब कीमत परिवर्तन एवं कुल व्यय परिवर्तन सदैव एक ही दिशा में चलते हैं तब माँग की लोच इकाई से कम होती है ।

उदाहरण द्वारा स्पष्टीकरण:

(a) इकाई के बराबर माँग लोच:

अर्थात् कुल व्यय अपरिवर्तित रहता है, अतः लोच इकाई के बराबर है ।

(b) इकाई से अधिक माँग लोच:

(c) इकाई से कम माँग लोच:

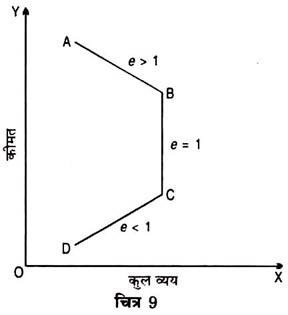
उपर्युक्त तीनों स्थितियों को चित्र 9 में प्रदर्शित किया गया है:

चित्र में A से B तक लोच इकाई से अधिक है क्योंकि कीमत के घटने पर कुल व्यय बढ़ रहा है तथा कीमत के बढ़ने पर कुल व्यय घट रहा है ।

B से C तक लोच इकाई के बराबर है क्योंकि कीमत के घटने या बढ़ने पर कुल व्यय में परिवर्तन नहीं होता ।

C से D तक लोच इकाई से कम है क्योंकि कीमत के घटने पर कुल व्यय घटता है और कीमत के बढ़ने पर कुल व्यय भी बढ़ता है ।

3. ज्यामिति रीति अथवा बिन्दु रीति (Geometrical Method or Point Method):

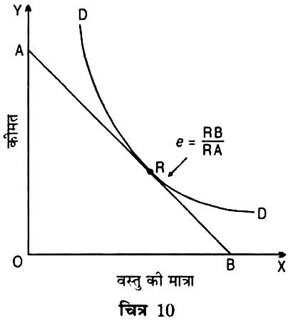
इस रीति द्वारा हम माँग वक्र से किसी बिन्दु पर माँग की लोच ज्ञात करते हैं । DD माँग वक्र के बिन्दु R पर माँग की लोच ज्ञात करने के लिए बिन्दु R पर स्पर्श रेखा AB खींची जाती है । AB का ढाल (Slope) और R बिन्दु पर DD वक्र ढाल एक समान है ।

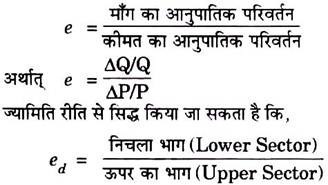
हम जानते हैं कि,

इस प्रकार बिन्दु रीति द्वारा माँग वक्र के किसी बिन्दु पर लोच ज्ञात करने के लिए उस बिन्दु पर खींची गई स्पर्श रेखा के निचले भाग (अर्थात् बिन्दु से X-अक्ष तक की स्पर्श रेखा द्वारा दूरी) को ऊपर के भाग (अर्थात् बिन्दु से Y-अक्ष तक की स्पर्श रेखा द्वारा दूरी) से विभाजित (Divide) करके बिन्दु विशेष पर माँग की लोच प्राप्त की जाती है ।

चित्र 10 में बिन्दु R पर माँग की लोच ज्ञात करने के लिए बिन्दु R पर AB स्पर्श रेखा खींची गयी है । RB निचला भाग (Lower Sector) तथा RA ऊपरी भाग (Upper Sector) है ।

अतः बिन्दु R पर माँग की लोच

इसी प्रकार माँग वक्र के विभिन्न बिन्दुओं पर स्पर्श रेखाएँ खींच कर बिन्दु रीति द्वारा माँग की लोच ज्ञात की जा सकती है ।

एक ही माँग वक्र के अलग-अलग बिन्दुओं पर माँग की लोच भी अलग-अलग होती है (Different Points on the Same Demand Curve have Different Elasticity of Demand):

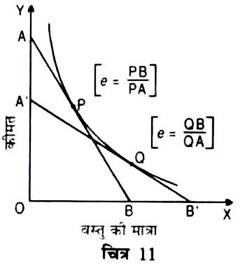
चित्र 11 में एक ही माँग वक्र DD पर P एवं Q दो अलग-अलग बिन्दु हैं ।

स्पष्ट है बिन्दु P तथा बिन्दु Q पर माँग की लोच एक बराबर नहीं है अर्थात् एक ही माँग वक्र के अलग-अलग बिन्दुओं पर माँग की लोच भी अलग-अलग होती है ।

माँग रेखा के सरल रेखा होने पर माँग की लोच की विभिन्न श्रेणियाँ (Various Degrees of Elasticity of Demand in a Straight Line Demand Curve):

एक सरल रेखा के रूप वाले माँग वक्र पर बिन्दु रीति की सहायता से माँग की लोच की सभी पाँच श्रेणियाँ प्रदर्शित की जा सकती हैं ।

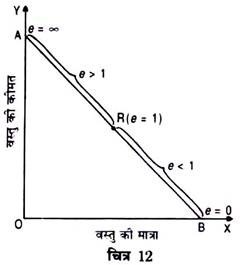
चित्र 12 में AB एक सरल रेखा है ।

(i) बिन्दु R पर माँग की लोच इकाई के बराबर है क्योंकि बिन्दु R पर नीचे का भाग (RB) ऊपर के भार (AR) के बराबर है (Lower Sector = Upper Sector) ।

(ii) बिन्दु A पर माँग की लोच पूर्णतया लोचदार होगी, क्योंकि बिन्दु A पर ऊपर का भाग शून्य है (Upper Sector is Zero) ।

(iii) बिन्दु B पर माँग की लोच पूर्णतया बेलोच होगी, क्योंकि नीचे का भाग इस बिन्दु पर शून्य है । (Lower Sector is Zero) ।

(iv) रेखा RB के मध्य प्रत्येक बिन्दु पर माँग की लोच इकाई से कम होगी क्योंकि इस रेखा के किसी भी बिन्दु पर नीचे का भाग ऊपर के भाग से कम होगा (Lower Sector < Upper Sector) ।

(v) रेखा AR के प्रत्येक बिन्दु पर माँग की लोच इकाई से अधिक होगी क्योंकि इस रेखा के प्रत्येक बिन्दु पर नीचे का भाग ऊपर के भाग से अधिक है (Lower Sector > Upper Sector) ।

उपर्युक्त विश्लेषण से स्पष्ट है कि एक ही माँग के विभिन्न बिन्दुओं पर माँग की लोच एक समान न होकर भिन्न-भिन्न होती है ।

4. चाप लोच रीति (Arc Elasticity Method):

जब कीमत परिवर्तन के कारण माँग की दशाओं में बड़ा परिवर्तन होता है तब माँग की लोच की सही माप ज्ञात करने के लिए चाप लोच रीति का प्रयोग किया जाता है । माँग की दशाओं में बड़े परिवर्तनों के कारण माँग की लोच का सही मूल्यांकन करने के लिए आरम्भिक एवं परिवर्तित मात्राओं का औसत प्रयोग किया जाता है । दूसरे शब्दों में, चाप प्रणाली द्वारा नयी एवं प्राचीन कीमत तथा माँग के औसत के आधार पर माँग की लोच निकाली जाती है ।

इस प्रणाली के अनुसार:

उदाहरण द्वारा स्पष्टीकरण:

तब माँग की लोच की सही गणना चाप रीति द्वारा निम्नलिखित रूप में की जायेगी:

उक्त उदाहरण में माँग की लोच की गणना यदि सामान्य सूत्र से की जाती है तब:

किन्तु यह माँग की लोच की सही माप नहीं है क्योंकि कीमत के परिवर्तन का माँग की दशाओं पर बहुत अधिक परिवर्तन एवं प्रभाव के कारण माँग की सही लोच चाप रीति द्वारा ही ज्ञात की जाती है । अतः माँग की सही लोच 3 है ।

ऋणात्मक चिह्न कीमत और माँग के विपरीत सम्बन्ध को बताता है । इसलिए माँग की लोच 3 (अर्थात् इकाई से अधिक) है ।