Income Determination with Government Sector

The below mentioned article provides an overview on income determination with government sector.

Simple Keynesian Model with Government:

In the simple Keynesian model of income determination we assumed that there is no government activity in the economy.

Let us relax this assumption to see how the equilibrium level of income can be determined in the presence of economic activity of the government. The government collects money from the economy and spends money into the economy. Government expenditures and receipts have an important effect on the economy.

Government budget has two sides — the expenditure side and the receipt side. Money inflows in the receipt side of the budget are of three types — taxation, public borrowing and sales of goods and services; money outflow in the expenditure side of the budget are also of three types—purchase of goods and services (G), transfer payment (T_r) and repayment of debts. Taxation is a compulsory contribution made by      the people to the government against which no direct payments are made by the government.

A taxpayer becomes poorer by the amount of taxes. Hence, the income available in the hands of the people is reduced by the amount of taxes paid. Public borrowing is made through the sale of new Government Bonds, which people voluntarily purchase. Neither their income nor their wealth is deduced thereby. They simply alter the form and composition of wealth in the private sector. An increase in the net indebtedness of the government to the central bank takes place through the creation of new money by the central bank.

Money-outflows from the government are of three types — transfer payments (T_r), government expenditure: on goods and services (G) and debt repayments. Transfer payments are made by the government to the people against which no services are rendered. For example, government subsidy to the public sector, unemployment benefit and’ similar payments belong to the category of transfer payments.

A transfer payment increases the disposable income of the people. Debt repayment does not make people richer, but it simply changes the composition of assets. The former bond holders have now money instead of bonds. Government expenditure on goods and services is made directly by the government which increases aggregate demand in the economic.

Let us now examine how the equilibrium level of income can be determined when the government activity in the economy is taken in to account. When there are government activities in the economy, aggregate demand will have three components: Consumption Expenditure (C), Investment Expenditure (I) and Government Expenditure on goods and services (G). Thus, the aggregate demand = C + I + G.

Let us assume again that investment expenditure – and government expenditure are autonomously given. Consumption expenditure is assumed to be a function of disposable income (Y_d) which is defined as (Y – T + T_r) where Y is income earned, T_r is taxes paid by the public and T is transfer payments received by the public from the government. It is assumed that taxes and transfer payments are independent of the level of income.

The equilibrium condition of income determination can be written as:

Y = C + I̅ + G̅ or, Y = C (Y – T̅ + T̅_r) + l + G

In this equation, T̅, T̅_r, I̅ and G are autonomous components. There is one unknown, Y, which can be determined from this equation. The level of y, which is satisfied by the above equation, is called the equilibrium level of income. The government expenditures have to be treated separately because they are not determined by the same variables as private expenditures.

The government expenditures are policy-determined and not uniquely related to any other variables in the model. The only change now would be in the specific equation of the IS curve, which shows equilibrium in the goods sector, would have to contain an additional term G, an exogenously determined term. It should be remembered that government activity is not confined to the acquisition of goods and services only; it also uses its power of transaction to acquire claims on resources from the private sector.

The equilibrium condition can be restated as:

Y – C = I + G or, S + T = I̅ + G

Equilibrium condition without a government was Y = C + I or, Y – C = I̅ or, S = I̅ which now should subdivide the claims to output into two parts — the claims to output of the private sector (Y -T) and the claims to output of the government sector T. Thus, we have S + T = I̅ + G, which is the alternative way of expressing Y = C + I̅ + G̅. S + T = I̅ + G and can also be written as S + (T – G) = I̅.

The term (T – G) may be called government savings while S refers to private savings. S + (T – G) is total saving (both public and private) and I represents total investment. We, thus, get a new version of familiar saving- investment relation.

We know that the equilibrium level of income is determined where W = J, where W is withdrawal and J is injection. The withdrawal W = S + T while the injection J = I̅ + G̅. When they are equal, the size of the circular flow remains unchanged and the level of income is said to be in equilibrium. Now, we assume that decisions about how much to consume are made on the basis of individual’s real income (Y).

The introduction of the government sector changes the relevant income, variable of the private sector decision-making from Y to (Y – T) = Y_d, disposable income. Using linear approximation, the consumption function becomes C = a + b(Y-T), where T represents the. taxes collected by the government. In most tax systems T is not exogenous but depends on Y, when Y changes, the amount of tax revenue collected by the government also changes, and, thus, disposable income (Y_d) changes.

Let us assume for simplicity a linear approximation for the relationship between taxes and income, such that T = t₀ + tY, where to is the amount of taxes which is independent of income (Y) and t is the marginal rate of taxes. Y – I is disposable income (Y_d) where T is the amount of tax revenue collected by the government.

Since the government also makes transfer payments, then T should be the net taxes collected, the difference between total taxes and total transfer payments, like taxes they affect- the economy via their effects on disposable income (Y_d). They should not be confused with government expenditures on goods and services.

Substituting the tax relationship into the consumption function, we have:

C = a + b (Y – t₀ – tY) = a + b [Y (1 – t) – t₀]…………… (1)

Equation (1) represents the consumption function on the assumption that desired consumption depends on Y_d, and taxes depend on total income (y).We assume that the introduction of the government sector does not change the investment function. Substituting the new consumption function from above and the old investment function (I = g₀ – g_r) to the new equilibrium condition for the goods sector, Y = C + I + G, we get:

Thus, equation (2) is an equation with two variables, Y and r, the other elements in this equation are either, government determined constants, t, to and G. or behaviorally determined constants a, go and g. This is the IS equation with multiplier 1/ 1 – b (1 – t). The equation summarizes the equilibrium condition for a goods sector, which now includes a government, and a relationship between two variables K and r. This is similar to the equilibrium condition for a goods sector without a government.

The multiplier and constant terms are different, but the meaning of the equation, new IS curve, is the same. We recall that the whole analysis of the interrelationships in the economy for which we used the IS curve did not depend on any particular value of the multiplier, or the other parameters of the IS curve.

Thus, we conclude that the introduction of the government sector into this model does not change any of our previous conclusions about the equilibrium conditions for the economy and the forces generated in the disequilibrium. However, we now have three added variables under government control which can bemused to affect the equilibrium value of income, employment, the price level and the interest rate, when these are these are not at a level consistent with some policy goal.

Different Budget Multiplies with Lump-Sum Taxes:

In the simple Keynesian model we know that when autonomous expen­diture changes, there will be a multiplier effect and the equilibrium income will change. Let us see how the equilibrium income changes when there are government activities.

We make the following assumption:

(i) The price level is’ fixed and money wages are rigid in the downward direction. Increase in expenditures is assumed to be reflected in increased output,

(ii) Aggregate real consumption expenditure is a function of real disposable income,

(iii) All taxes are lump-sum taxes which are independent of income and

(iv) The consumption function is linear.

Suppose C = a + b (Y – T) is the consumption function where 0 ˂ b ˂ 1 and a ˃ 0. The Equilibrium condition can be written as Y = C + I̅ + G̅ or, Y = a + b (Y – T) + I + G. Differentiating both sides with’ respect to G and assuming that T and I remain constant, we get

Budget Adjustment with Income-Tax:

Now we assume that, income-tax is not autonomously given as above but is a function of income. We consider a linear proportional tax function T= t. Y where t represents the marginal rate of tax. The disposable income is now equal to Y – T = Y – tY = Y (1 – t) We assume, as before, a linear consumption function: C =a + b (1 – t) Y. The slope of the consumption function is now (1 – t). Note that in the ease of lump-sum tax, the slope of the consumption function does not change, but only the vertical intercept changes. But in the case of income-tax, slope of the consumption function changes, while the intercepts remain the same. Assuming linear consumption function, as before, and lump-sum taxes, T, we get the consumption Function as:

C = a + b(Y – T) or C = (a – bT) + bY which shows that, when the lump-sum tax is imposed the intercept of the consumption function is reduced to (a — bT) but the slope remains unchanged. In the case of the linear and proportional tax function f = t. Y, the consumption function becomes C = a + b (1 – t)Y which shows that as a result of the imposition of the tax the intercept of the consumption function remain constant at a’ but the slope decreases to b (1 – t) and the consumption function become flatter.

The equilibrium condition in the commodity market is:

Y = C + I + G̅ or Y = a + b (1 – t) Y + I̅ + G̅

It is assumed that the investment expenditure and government expenditure are autonomously given. We can now consider the effect of budget adjustments on the equilibrium level of income. Consider the effect of ∆G with the tax yield remaining constant. Since the tax yield is unaffected, there is no difference between lump-sum tax and an income-tax.

The level of income will increase and the multiplier effects can be shown as:

dY = 1/1 – b dG = multiplier is greater than one. It is the same as we obtained in the case of lump-sum taxes. However, with the increase in income, the tax yield may remain constant if the rate of tax decreases.

We now consider the effect of change in G with the tax rate remaining constant. In this case,

The multiplier is now equal to 1/1- b (1-t) which is smaller than the multiplier 1/1-b, because here the tax yield T increases with income and does not remain unchanged. In the case of a lump-sum tax when the level of income increases with increase in G, the tax yield does not increase. But in the case of income- tax as the level of income increases the tax yield increases as well. Hence, the multiplier effect is higher in the case of lump-sum tax than in the case of income-tax.

If we now consider the effect of change in tax yield holding G unchanged, then we get: dY/dT = – b/1-b or, dY = -b/ 1-b or dT. This means that as the tax yield increases, the level of income decreases and vice versa. The balanced budget case is one where we make equal changes in G and T. The effect of change in G and T can be obtained by adding separate effect of changes in G and T.

We have seen that dY = 1/1-b dG, when only government expenditure changes and dY = -b/1-b dT when only the tax changes. When both G and T change by the same amount, dG = dT and dY = 1/ (1-b) dG + -b/ (1-b) dG.

dY = dG = dT.

This is the balanced budget multiplier which is unity, as we have proved before. If government expenditure and taxes increase by the same amounts, so that the budget is balanced, level of income will increase by the amount of the government expenditure. We consider the effect of change in t with G remains unchanged on the equilibrium level of income.

The equilibrium condition can be written as:

Y = a + b (1 – t) Y + I̅ + G̅ or, Y = a + bY-btY + I̅ + G̅

Differentiating both sides with respect to t, we get:

The multiplier now depends on the initial level of income and tax rate. The lower the initial rate of tax, the greater will be the rate of increase in income. Thus, when the tax rate is changed, its effect in the level of income depends on the initial tax rate and the level of income.

During a period of depression we require the same type of budget adjustment, whether we use lump-sum tax or income-tax. The level of income can be increased either by a decrease in taxes, government expenditure remaining the same or, by increasing government expenditure, the tax yield remaining unchanged or, by a change in tax rate, government expenditure remaining unchanged.

Balanced Budget Multiplier: Diagrammatic Presentation:

The budget is said to be balanced when the tax yield is equal to government expenditure. If G = T and then ∆G = ∆T in any period then the budget will continue to be in balance. The multiplier effect of equal change in T and G is known as balanced budget multiplier. Our assumptions here is the same as in previous section.

The equilibrium condition can be written as: Y = C + I +G where consumption function C = a + b (Y – T), the balanced budget multiplier can be obtained as follows: Y = a + b (Y – T) + l + G. When G changes and T remains unchanged we get dY/dG = 1/1-b or dY = 1/ (1-b) dG.

Again, when T changes and G remains unchanged, we get:

dY/dT = -b/1-b or dY = -b/1-b dT.

When both G and T change at the same time we get dY = 1/(1-b) dG + -b/(1-b)dT.

In this case of equal change in G and T, we get dG = dT, where dY = (1-b)/(1-b) dG.

Thus, when dG = dT, we have dY = dG = dT.

This is the famous balanced budget multiplier. The balanced budget multiplier can also be represented in Fig. 11.1. In the case of lump-sum tax, the slope of the consumption function remains unchanged, while the vertical intercept changes. The consumption function, before tax, can be written as C = a + bY and, after tax, it becomes C = a + b(Y – T) = (a – bT) + bY. Here the slope remains the same but the intercept changes.

In Fig. 11.1 income is measured on the horizontal axis and expenditure on the vertical axis CD = aggregate demand = C + I + G prior to tax and ON is the initial equilibrium: level of income. Now a tax is imposed by the amount ML and the vertical impact of the consumption is reduced to OA and the aggregate demand is now AB.

Expenditure of GL is made equal to tax yield ML. Thus/the aggregate demand curve shifts to the position EF with the level of income OH. Consumption expenditure is at HL and the increase in income NH = ML = GL. Thus, the balanced budget multiplier holds good for 1: 1 expansion in income.

To obtain the balanced budget multiplier for income-tax, we assume that the tax yield, T, depends on income. For simplicity’s sake we assume linear proportional tax function: T = t. Y where t is the rate of tax. The disposable income is given by Y – tY = (1-t) Y. The consumption function is assumed to be linear: C = a + b (1 – t)Y. In the case of the income-tax the slope of the consumption function is changed but the intercept remains unchanged. The equilibrium condition can be written as:

Y = C + I̅ + G̅ or, Y = a + b(1 – t) Y + I̅ + G̅.

We now consider the effect of-change in assuming that the tax yield remains unchanged. When the tax yield remains constant, there is no difference between the income-tax and the lump-sum tax. The equilibrium condition can be written as Y = a + b(Y – T) + I̅ + G̅. Differentiating both sides with respect to G, and rearranging we get dY = 1/1-b dG.

Now, G remains unchanged and the tax yield changes. This can be obtain as:

Y = a + b (Y – T) + I̅ + G̅

Differentiating both sides with respect to T, and rearranging, we get, dY = -b/(1 – b) dT. The effect of change both T and G can be obtained by adding the separate effects of change in G and T, i.e.

Thus, the balanced budget multiplier in the case of income-tax is also unity. The balanced Budget multiplier of income-tax can be represented in Fig 11.2.

Let the aggregate demand curve be A’C’ before tax. After the income-tax is imposed the slope of the consumption function is reduced though the vertical intercept remains unchanged. A tax rate t = N’H’/ON’ is imposed and the aggregate demand A’C’ pivots to A’B’. Now, public expenditure is increased by L’G’ which is equal to M’L’ which shifts the aggregate demand function to D’E’ though the consumption expenditure initially remains unchanged at M’N’ = L’H’. Thus, the increase in income, N’H’, is equal to the increase in government expenditure, L’G’, which is equal to increase in tax yield, M’L’. Thus the balanced budget multiplier, for income tax is also obtained.

Stabilization and Balanced Budget:

We know the effect in change in investment expenditure on the equilibrium level of income. If we now assume that all taxes are lump-sum taxes and T is autonomous, the investment multiplier is equal to 1/1 – b.

Since Y = a + b(Y – T) + I̅ + G̅ .^.. ∆Y = b∆Y + ∆I .^.. ∆Y = 1/(1 – b) ∆I.

Now we assume that, taxes vary with income T = T(Y) and it is a linear function of income T = tY, where t is a marginal tax rate.

Hence Y = a + b(Y – tY) +  I̅ + G̅ or, Y = a + b (1 – t) Y +  I̅ + G̅

.^.. ∆Y = b (1 – t) ∆Y + ∆I .^.. ∆Y = 1/1 – b (1 – t) ∆I

The investment multiplier is equal to 1/1 – b (1 – t) which is less than 1/1 – b. This means that the multiplier effect of a change in investments is lower when there is automatic flexibility, than when there is none, because, in the absence of automatic flexibility there is only one leakage from the circular flow — the saving. But, in the presence of automatic flexibility, there are two leakages — the saving and the tax.

As the level of income rises due to increase in investment, taxes also increase which puts a brake on the expansion in the level of income. When tax is a function of income, the expansionary effect of an increase in investment is lower than when it is not a function of income.

Expansionary Effect of Change in Investment with Unbalanced Budget:

Suppose the budget is initially balanced. Now, investment increases — which also increases income and this increase in income will increase tax yield. As G remains unchanged, a surplus budget will emerge.

Now we assume that an increase in investment is associated with a balanced budget, which means T = G.

Then Y = a + b (Y – T) +  I̅ + G̅ or, Y = a + b(Y – tY) +  I̅ + tY or Y – b(1 — t)Y — tY = a +  I̅. Rearranging, we get Y = a + I/1 – b(1 – t).

.^.. ∆Y = 1/(1 – b)(1 – t) x ∆I. The multiplier associated with the change in investment is 1/(1 – b)(1 – t) and this is greater than the previous multiplier 1/1 – b(1 – t). This means that, when private investment increases and taxes also vary with income, the level of income will increase more when the budget is balanced than when it is unbalanced (deficit).

Similarly, in the case of decrease in investment, the decrease in income will be larger when the budget is balanced than when it is not balanced. Thus, the balanced budget reinforces expansionary or contractionary tendencies. This implies that, the aim of income stabilization is not compatible with the requirement of the balanced budget.

Furthermore, the balanced budget policy of the government may aggravate these fluctuations, rather than eliminate it. The balanced budget policy is, therefore, not a sound
policy from the point of view of stabilization. Our advice to the government in this respect is to produce a surplus budget in a period of economic prosperity and a deficit budget in a period of severe recession.

A Deficit Budget and Multiplier:

It is commonly believed that a deficit budget is always expansionary It is not always true. Budget deficit may not be expansionary and there is no unique deficit multiplier. Let us start with a balanced budget situation and then consider the effect of deficit budget. We now assume that the government expenditure is increased by ∆G with taxes remaining unchanged. There is then a budget deficit by ∆G. Income increases by ∆Y such that ∆Y = 1/(1 – b) ∆G. Here the multiplier is 1/(1 – b).

Now, suppose that the government reduces taxation by the amount ∆T. with G remaining unchanged. There is a budget deficit of ∆T and the level of income increases by ∆Y = -b/(1 – b) ∆T. The multiplier here is –b/(1 – b). Again assume that, the government now increases transfer payments by ∆T_r which is larger than ∆T, whereas G remains the same. The budget deficit is equal to ∆T_r – ∆T. Let us see how it effects the equilibrium level of income. Since Y = a + b (Y – T + T_r) +  I̅ + G̅

.^.. ∆Y = b (∆Y – ∆T + ∆T_r) = -b/(1 – b) (∆T_r – ∆T)

In this case also the multiplier is equal to –b/(1 – b).

Suppose that the government expenditure is increased by ∆G which is greater than the increase in ∆T, transfer payments do not change. The budget deficit is now ∆G – ∆T. Consider its effect on the level of income.

We know that ∆G > ∆T and the budget deficit is expansionary. But 1/(1 – b) is not the multiplier in this case as the deficit here is (∆G – ∆T) and not (∆G – b∆T).

Lastly, suppose that this time the government reduces taxation by an amount ∆T x G, transfer payments remain the same. The budget deficit is ∆T – ∆G. Hence, the change in income may be given by ∆Y = 1/(1 – b) (∆G – b∆T). Note that, ∆Y may be negative or positive. It will be negative when Note that, ΔY may be negative or positive. It will be negative when |ΔG| > |bΔT|, even when there is a deficit in the budget and the level of |ΔGT| = |bΔT|, ΔY = and the level of income remains unchanged. This analysis show that the budget deficit is not always expansionary. It could be contractionary or even neutral.

Built –In Stability of the Tax-System:

We have seen in a simple economy without government the investment multiplier is given by dy = 1/(1-b )d1 where b is the mpc (0 < b < 1) .This shows that fluctuations in autonomous investment leads to fluctuations in the level of income. Now, the question is whether this fluctuations in the level of income can be controlled by the government’s activity in the economy. If the government’s budget contain a mechanism to control that fluctuations then it is said that a built-in-flexibility exists in the budget.

We take the following assumption to see how the existence of a built-in-flexibility leads to smaller functions:

(1) Taxes depend on the level of income, such that, as the level of income increases, total tax yield also increase. The tax is a linear and proportional function of income, i.e. T = tY, Where t is marginal tax rate.

(2)Government’s expenditure is autonomously given.

(3)The consumption is a linear function of disposable income: C = a + b (Y – tY).

(4) Investment is autonomously given.

(5) The economy is a closed economy.

The equilibrium condition of income determination can be written as

Y = C +  I̅ + G̅ or, Y = a + b (1 – t) Y +  I̅ + G̅

The differentiating both sides with respect to I and rearranging, we get dy = 1/1-h(1-t) d1. The investment multiplier is equal to 1/1-b(1-t) whereas the investment multiplier without Government, or when taxes are autonomous given can be written as 1/(1-b) .It is clear that, 1/(1-b) > 1/1-b(1-t). This means that, the multiplier effect of change in autonomous investment will be lower when taxes are a function of income than when they are not.

Thus, it can be said that when taxes very directly with the level of income, there is built-in- flexibility in the budget which regulates fluctuation in the economy. The mechanism works as follow: Suppose investment expenditure increases and, as result, the level of income also increases, the tax collection also increases. As tax revenue increases, the level of income decreases. Thus the original increase in income is dampened and, hence the level of income is reduced when there is built-in- flexibility in the budget.

Now the question is: how can we measure the effectiveness of built-in-flexibility? Following Musgrave, we can suggest the measure of the effectiveness of built-in-flexibility as follows: Let dY_A is the change in the absence of built-in-flexibility and let dY is the change in income in the presence of built-in-flexibility. Then dY_A = 1/(1 – b) dI and dY = 1/1 – b (1 – t) dl. Then g = 1 –dY/dY_A may be taken as a measure of the effectiveness of built-in-flexibility, where 0 < g < 1. When g = 0, dY = dY_A, the change in the level of income will be the same both in the absence and in the presence of built-in-flexibility. So, the built-in-flexibility is ineffective. If g = 1, dY = 0, the level of income remains constant and does not change at all even if investment changes. This means the built-in-flexibility is completely effective. The greater the value of g the greater will be the effectiveness and vice versa

This means that the effectiveness of built-in-flexibility depends on two factors: the mpc = (b) and mtr = t. Apart from the mpc, g, depends on the elasticity of the tax function. For example, if t = 1, then entire increase in income is taken away in the form of tax collection, which means that the marginal rate of tax (Mrt) is 100%. In this case, when t -1, g = b and since mpc < 1, it follows that g < 1. This means that so long as the mpc is less than unity built-in-flexibility cannot be perfect to keep the level of income perfectly stable.

Government Budget in the IS-LM Model:

So far we have been discussing government activities on the simple Keynesian model of income determination. Now we wish to incorporate government activities in the IS-LM Model. The equilibrium condition in the commodity and money market can be written, respectively, as:

(1) S (Y_d) + T = S(Y – T) + T = I(r) + G

(2) M = L (r, Y), where ƏL/Ər < 0, δL/δY > 0 and T, G and M are autonomously given.

Hence, in the above two equations, we have only two unknowns: r and Y. Thus, solving these two equations simultaneously we can determine equilibrium income and interest rate. Equation (1) gives us the IS curve and Equation (2) gives the LM curve. The IS curve represents the combination of r and Y for which S + T = I + G is satisfied; whereas the LM curve represents the combinations of r and y for which the demand for money is equal to the supply of money or M = L(r, Y).

It should, however, be noted that when the government activities are introduced the equation of the IS curve is affected, whereas the equation of the LM curve remains unchanged. The introduction of the government activities do not change the slope of the IS curve, so long all taxes are lump-sum taxes and government expenditure is autonomously given, the equation of the IS curve becomes:

S(Y – T) + T = I(r) + G.

By differentiating both sides we get S’dY = I’dr or dr/dY = S’/I’ which is the same as when the government activities are not introduced. Thus, the IS curve shifts parallel when G and T are autonomous. Since G and T enter the equation of the IS curve, the position of the IS curve will shift if G and T changes. Thus, if T decreases (increases), the IS curve shifts to the right (to the left), G remaining unchanged, on the other hand, if G increases (decreases), T remaining the same, the IS curve shifts to the right (to the left). Thus, in our model, the tax-expenditure policy of the government will change the equilibrium level of income and the interest rate by affecting the IS curve only.

We can obtain the effect of ∆G or ∆T by differentiating equations (1) and (2) with respect to G or T and solving for dY/dT and dr/dT (or dY/dG and dr/dG). Differentiating equations (1) and (2) with respect to T, we can get the effect of ∆T, with G and M remaining unchanged.

On the assumption that 0 < S’ < 1, Ly> 0, L_r < 0 and I’ < 0, it follows dr/dT < 0 and dY/dT < 0. This means that when T increases (decreases), G remaining the same the equilibrium level of income decreases (increases), and the rate of interest also decreases (increases). Geometrically, this can be shown in the Fig. 11.3, when C remains unchanged and T increases, the IS curve shifts to the left from IS₀ to IS₁, the LM curve remains the same.

As a result the equilibrium income and interest rate decreases from Y₀ to Y₁ and r₀ to r₁, respectively as in Fig. 11.3. Similarly, when T decreases, G remains unchanged, the IS curve shifts to the right from IS₀ to IS₂ and Y and r will increase from Y₀ to Y₂ and r₀ to r₂.

However, in a limiting case of the liquidity trap situation where L_r →, dY/dT = -(1 – S’)/S’ < 0 and dr/dT = 0. In this situation, if T increases, Y decreases but r remains the same.

Diagrammatically, this can be represented in Fig. 11.4, when L_r → ∞ the LM curve is horizontal (liquidity trap situation). Now, if the IS curve cuts the horizontal part of the LM curve and the IS curve shifts to the left, then it is obvious that the level of income falls but the interest rate remains unchanged. We can now consider the effect of change in C, T remaining unchanged. Differentiating equations (1) and (2) with respect to G we get

If G increases (T remaining unchanged) the equilibrium level of income increases from Y₀ to Y₂ and the interest rate will increase from r₀ to r₂, in Fig. 11.3, as IS curve shifts to the right from IS₀ to IS₂ In a special case, where the IS curve cuts the horizontal part of the LM curve, L_r → ∞ and dY/dG = I/s’ and dr/dG = 0. The level of income increases but the rate of interest remains the same. Now we consider the balanced budget multiplier when both G and T change by equal amounts their combined effect on income can be obtained by taking the sum of their individual effects. Thus,

So long as I’ < 0, S’ > 0. Ly >0 and L_r < 0 the balanced budget multiplier is positive but less than unity. However, in a limiting case, where investment function is completely interest inelastic, or, if the money demand function is perfectly interest elastic, i.e., if I’ = 0 or L_r → ∞ then dY/dG + dY/dT = 1, the balanced budget multiplier is unity.

In the IS-LM model we can consider the effect of change in money supply on equilibrium level of income and interest rate, assuming that G and T remain unchanged. Differentiating equations (1) and (2) with respect to M and solving for dY/dM and dr/dM we get: S’ dy/dM – I’ dr/dM = 0 and L_y dY/dM + L_r dr/dM = 1.

Solving these equations with the help of Cramer’s rule we get

This shows that, if money supply increases the equilibrium level of income increases but the interest rate decreases. If money supply increases the LM curve shifts to the right, assuming that the IS curve remain unchanged. However, if L_r →, dY/dM = 0 and dr/dM = 0. In this liquidity trap situation, monetary policy become completely ineffective. Lastly, consider the combined effect of equal change in G and M on income when T remains unchanged.

This is given by dY/dG + dY/dM = L_r + I’/S’L_r + I’L_Y > 0. In this case, we can make a comparison between the effects of tax-financed increase in G and financing increase in G by money creation. In the former case we get dY/dG + dY/dT = S’L_r/ I’/S’L_r + I’L_Y and in the latter case we get dY/dG + dY/dM = L_r + I’/S’L_r + I’L_Y.

Now, by mathematical manipulation we get, = (I-S’)L_r + I’/S’L_r + I’L_Y > 0. This means that, dY/dG + dY/dM = dY/dG + dY/dT which means that, the expansionary effect of an increase in G financed by an equal increase in M will be higher than the expansionary effect of an increase in G financed by an equal increase in T.

This can be shown in Fig. 11.5 where both the IS and LM curves shift to the right; in the first case, where income increases from Y₀ to Y₁ and r₀ remains unchanged. But in the second case, only the IS curve shifts to the right by a small amount when the LM curve remains unchanged. Thus, Y increases by Y₀ to Y₁ and r increases from r₀ to r₁.

So far, our assumption was that all taxes are lump-sum and autonomous. We now introduce an income-tax instead of lump-sum tax. Let T = tY be the tax function where t is the marginal (and also average) tax rate. When the tax function is T = tY, the slope of the IS curve is now affected.

This is shown as follows:

This shows that, as G increases, the equilibrium level of income and the interest rate increases. The results are similar in the case of lump-sum taxes, but the multiplier are smaller than in the case of lump-sum taxes.

Similarly, we can find the value of dY/dM, dr/dM, dY/dt and dr/dt. Then we can also get IS and LM curves similar but complicated multiplier results.

Fiscal Policy and Crowding out Effects:

Fiscal policy shifts the IS curve. A fiscal expansion shifts the IS curve to the right and a fiscal contraction shifts it to the left. The multiplier, in the commodity market, associated with the change in G is the reciprocal of the MPS, assuming lump-sum taxes. That is, dY/dG = 1/S’ where S’ the MPS. The multiplier in the IS-LM model with lump-sum taxes is: dY/dG = L_r/S’L_r + I’L_Y = 1/S’ + I’L_Y. We can see that the multiplier in the IS-LM model is smaller than in the simple Keynesian model. That is 1/S’ + I’L_Y < 1/S’.

This result can be explained as follows:

When G increases the level of income and interest rate increases. At unchanged rate of interest, increase G increases the level of aggregate demand. To meet the increased demand, output must rise as shown by the shift in the IS schedule. At each rate of interest, equilibrium income must rise by multiplier times G.

If the economy is initially in equilibrium at point E as in Fig. 11.6, and G rises, we would move to point E” with unchanged interest rate. At E” goods market is in equilibrium where planned spending equals output. But the asset market is not in equilibrium. Income has increased and, thus, the quantity of money demanded is higher. Since there is excess demand for money, the interest rate rises. Firm’s planned investment spending declines at higher interest rates, and, thus, aggregate demand decreases.

The new equilibrium is at point E’. The increase in income (Y₁ – Y₀) is less than the amount indicated by the simple multiplier (Y₂ – Y₀) because, higher interest rate crowd-out some investment spending. We assume that the money market clears quickly and continuously, while output adjust only slowly. This implies that, as government spending increases, we stay initially at point E, as there is no disturbance in the money market.

The excess demand for goods leads firms to increase output, and that increase in output and income raises demand for real balances. The resulting excess demand for money, causes interest rate to rise, and we proceed up along the LM curve with rising output and rising interest rates, until we reach the new equilibrium at E’.

Crowding-Out and the Different Shape of the LM Curve:

Comparing E’ to initial equilibrium at E, we see that increased G raises both income and interest rate. But another comparison is between E’ and E”, the equilibrium in the commodity market with unchanged interest rates. Comparing E” and E’ it becomes clear that the adjustment of interest rates and their impact on aggregate demand dampen the expansionary effect of increased G.

Income increases to Y₁ rather than to Y₂ because the rise in the interest rate from r₀ to r₁ reduces the level of investment spending. Thus, we can say that, increase in G crowds out private investment. Crowding out occurs when expansionary fiscal policy causes interest rates to rise, thereby reducing private investment spending.

What factors determine how much crowding out takes place?

The different IS and LM curves show the following:

The Halter LM curve will increase income more and interest rates less. The flatter curve will increase income and interest rates less. Income and interest rates increase more the larger the multiplier and, thus, the larger the horizontal shift of the IS curve.

In each case the extent of crowding out is greater than the more interest rate increases when G rises.

The magnitude of the crowding out depends on the interest sensitivity of investment function (I’) and the interest sensitivity of the money demand function (L_r). The greater the value of I’ and lower the value L_r, the greater will be the crowding out effect and vice versa. Two extreme cases are: the liquidity trap and the interest inelasticity of investment function, where there is no crowding out effect.

The Liquidity Trap and Crowding Out Effect:

In the liquidity trap situation where the LM curve is horizontal, an increase in G has its full multiplier effect on the equilibrium level of income. There is no change in the interest rate associated with the ∆G, and, hence, no investment spending is crowded out. This can be shown in Fig. 11.7(a) below where LM curve is horizontal, monetary policy has no impact on the economy and fiscal policy has a full effect. If the demand for money is very sensitive to the interest rate, so that the LM curve is horizontal, fiscal policy is effective and monetary policy is ineffective as Fig. 11.7(a) shows as IS shifts from IS₀ to IS₁.

If the LM curve is vertical, then increase in G has no effect on the equilibrium level of income and it increases the interest rate only. In this case an increase in G shifts the IS curve to IS’ but has no effect on income. If the demand for money is not related to interest rate, as a vertical LM curve implies, then there is a unique level of income at which the money market is in equilibrium as Fig. 11.7(b) shows.

Crowding Out and the Classical Case:

When the LM curve is vertical an increase in G cannot change the equilibrium level of income and only raises the equilibrium interest rate which will offset private spending. In this case, the increase in interest rates crowds out an amount of private spending equal to an increase in government spending. Thus, there is a full crowding out if the LM curve is vertical. In Fig.11. 7(b), we show complete crowding out.

Is Crowding out a Possibility:

To consider the possibility of crowding out three points must be made. The first point is that, if we consider an economy below full-employment and given prices, then fiscal expansion will increase output. But when we talk about fully employed economy, crowding out becomes a possibility because output cannot then be increased. In such situations an increase in demand will increase the price level rather than an increase in output.

Second point is that, in an economy with unemployed resources there will not be lull crowding out because the LM curve cannot be vertical. A fiscal expansion will raise interest rates and income. Crowding out is, thus, a matter of degree. The increase in aggregate demand raises income which raises the level of saving which again makes it possible to finance a larger budget deficit without completely displacing private spending.

We can explain this with the help of the following equation:

S = I + (G +T_R – T_A). Here the term G + T_R – T_A is the budget deficit. Now an increase in deficit must lower investment, given saving. When the deficit rises, the government has to borrow to pay for its excess spending which comes from households saving, leaving less available for private investment. But if saving rises with government spending as income increases, then there need not be complete crowding out of private investment.

The third point is that, with unemployment, interest rates may not rise at all when the fiscal expansion is accommodated by the monetary authority by increasing money supply. Monetary policy is accommodating fiscal ex­pansion when the money supply is increased to prevent interest rates from increasing. This accommodation policy of the central bank is also referred to as monetizing budget deficits which shifts the IS and LM curves to the right, as in Fig. 11.8. Income will definitely increase, but interest rates remain unchanged and, thus, private investment will not be adversely effected.

Effectiveness of Monetary and Fiscal Policy:

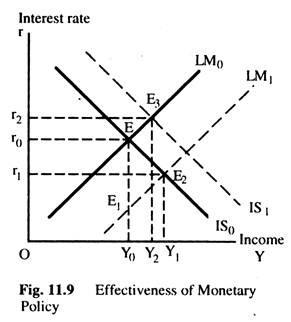
We can compare the relative effectiveness of fiscal and monetary policy with the help of a simple model. By monetary policy we mean the changing of the supply of money by the monetary authority without directly altering current income stream. Monetary policy will affect the position of the LM curve through changes in money supply, as shown in Fig 11.9.

An increase in the real money stock shifts the LM curve to the right to LM₁ and the asset markets adjust immediately through decline in interest rate between points E and E₁. The lower interest rates stimulate investment and other expenditures and increase income until a new equilibrium is reached at E₂. This shows that a rise in real money stock increases equilibrium income and lowers equilibrium interest rates as Fig. 11.9 shows.

By fiscal policy we mean the change in government expenditure (∆G) and taxation. We assume that ∆G without any change in money supply with the public. A tax-financed expenditure or a deficit financed by a sale of bonds to the public may be used as an example of fiscal policy. In short, pure fiscal policy operates through AG and, thereby, affecting the IS with no effect on the LM curve, as the Fig. 11.9 shows, when IS₀ shifts IS₁ and LM₀ remains unchanged and both income and interest rates increase to Y₂ and r₂, respectively.

Now we examine the effectiveness of monetary policy with the different shape of the LM curve. The horizontal portion (perfectly interest-elastic demand for money) is called the Keynesian range while the vertical portion is called the Classical range. The upward rising portion is the Intermediate range.

Suppose the money supply increases and the LM curve shifts to the right The effect of monetary expansion will depend on the point of intersection of the IS curve with the different range of the LM curve as shown in Fig. 11.10.

(a) If the IS curve (IS₀) intersects the LM curve at the latter s horizontal portion, then the change in money supply will have no effect on income and interest rate. In the Keynesian range, in the liquidity trap situation, the monetary policy is completely ineffective.

(b) The intersection of the IS curve (IS₂) with the LM curve at the latter’s vertical portion — the classical range—where the speculative demand for money is zero. The entire increase in money supply will be absorbed by the transaction demand for money. This will happen when money income increases either due to increase in price level or increase in real income. The interest rate falls because the increase in money supply will induce people to use this extra money to buy bonds. This will increase bond prices which means a fall in the rate of interest.

(c) If the IS curve (IS₁) cuts the LM curve in its intermediate range, an increase in money supply will increase the level of income and decrease the rate of interest. The rate of interest will fall and the level of income will rise less than in (b) because, in (b), the rate of interest falls enough to absorb the whole addition to the supply of money into transactions, while, in (c), a part of the increase will be absorbed into speculative holdings.

We now consider the effectiveness of fiscal policy. Suppose G increases while the money supply remains unchanged. The IS curve will shift to the right. Here also the effect of fiscal expansion will depend on the intersection of the IS and LM curves. This is explained in Fig 11.11 where we again get three situations.

(a) If the new IS₀ curve (IS₀‘) intersects the LM curve in the Keynesian range, the level of income rises by the full amount of the multiplier effect. The rate of interest remains unchanged and the fiscal policy is perfectly effective.

(b) In the classical range where IS curve shifts from IS₂ to IS₂’ the level of income remains constant at Y₂ and the rate of interest rises from r₂ to r₂ In this range fiscal policy is not effective at all.

(c) If the IS curve cuts the LM curve in the intermediate range and the IS curve shifts from IS₁ to IS₁’, the level of income rises from Y₁ to Y₁‘ and the rate of interest also rises from r₁ to r₁’. The increase in the level of income is not as high as in the Keynesian range. Similarly, the increase in the rate of interest is not as great as in the classical range. The effectiveness of fiscal policy is in between the two extreme cases.

Policy Debate:

Some economists view the economy as inherently unstable and argue that the economy experiences frequent shocks to aggregate demand and ag­gregate supply. Unless policymakers use fiscal and monetary policy to stabilize the economy these shocks will lead to unnecessary fluctuations in output, employment and price level. According to the popular saying, macroeconomic policy should stimulate the economy when it is depressed and slowing the economy when it is overheated.

Other economists consider the economy as naturally stable and blame bad economic policies for the large fluctuations of the economy. They argue that economic policy should not try to “fine tune” the economy. Instead, policymakers should recognise their limitations and be satisfied if they do no harm.

This debate has continued for many years and the fundamental issue now is how policymakers should use the theory of economic fluctuations. We now ask two questions that have arisen in this debate: First, should monetary and fiscal policy take an active role to stabilize the economy, or should policy remain passive? Second, should policymakers be free to use their discretion in responding to changing economic conditions or should they be committed to following a fixed rule?

Should Policy be Active or Passive?

Economic policymakers consider stabilisation as one of their primary responsibilities. When government is considering a major change in fiscal or monetary policy, foremost in the discussion amongst the policymakers are whether the change will influence inflation and unemployment and whether aggregate demand needs to be stimulated or depressed.

Although the government has long conducted monetary and fiscal policy, the view that it should try to stabilize the economy is more recent. To many economists the case for active government policy is clear and simple. The model of aggregate demand and aggregate supply shows how shocks to the economy cause recession. It also shows how monetary and fiscal policy can prevent recessions by responding to these shocks.

These economists consider it wasteful not to use these policy instruments to stabilize the economy. Other economists are critical of the government’s attempts to stabilize the economy and argue that the government should take a “hands off” approach to macroeconomic policy. At first, this view might seem surprising. To find out why these critics want the government to refrain from using monetary and fiscal policy to stabilize the economy, let’s consider some of their arguments.

Lags in Implementation and Effect of Policies:

Economic stabilization would be easy if the effects of policy were immediate making policy would be like driving a car, policymakers would simply adjust their instruments to keep the economy on the desired path. Driving a car changes direction almost immediately after the steering wheel is turned.

But economic policymakers face a problem similar to that of a pilot of a large ship because a ship changes course long after the pilot adjusts the rudder. Like a ship’s pilot, economic policymakers face the problem of long lags. Indeed, the problem for policymakers is even more difficult, because the lengths of the time lags are hard to predict. These lags greatly complicate the conduct of the government policy.

Economists distinguish between two lags in the conduct of Stabilization Policy: the inside lag and the outside lag. The inside lag is the time between a shock and the policy action that responds to that shock. This lag arises because it takes time for policymakers first to recognise the shock and then to put appropriate policies into effect.

The outside lag is the time between a policy action and its influence on the economy. This lag arises because policies do not immediately influence income, spending and employment. Fiscal policy has a long inside lag because, changes in spending or taxes require legislation and the legislative process is often slow and cumbersome. These delays make fiscal policy an imprecise tool for stabilizing the economy.

Monetary policy, on the other hand has a long outside lag. It works through interest rates, which in turn influence investments. But many firms make investment plans far in advance. Thus, a change in monetary policy is thought not to affect economic activity until about six months after it is made.

The long and variable lags associated with fiscal and monetary policy make stabilising the economy difficult. Advocates of passive policy argue that, because of these lags, successful stabilisation policy becomes an impossible task. Indeed, attempts to stabilise the economy are too often destabilizing. Suppose the economy’s condition changes between the time when action is taken and the time when it affects the economy.

Thus, active policy may end up stimulating the economy when it is overheated or depressing the economy when it is cooling off. Advocates of active policy admit that, such lags do require policymakers to be cautious. However, they argue, these lags do not necessarily imply that policy should be completely passive, especially in the face of severe economic downturn.

Automatic stabilisers are designed to reduce the lags associated with the stabilisation policy. Automatic stabilisers are policies that stimulate or depress the economy when necessary without any deliberate policy change. For example, as we have already seen, the system of income-tax automatically reduces tax revenue when the economy goes into a recession, without any change in the tax laws, because individuals and corporations pay less tax when their incomes fall.

Similarly, the unemployment benefits and other welfare payments automatically raise transfer payments when the economy move into a recession. We can view these automatic stabilisers as fiscal policy without any inside lag.

Economic Forecasting:

Since policy influences the economy after a substantial lag, successful stabilisation policy requires the ability to predict accurately future economic- conditions. If we cannot predict correctly what will happen in six months or a year, we cannot decide whether monetary or fiscal policy should be used to expand or contract aggregate demand. Unfortunately, economic developments are unpredictable, at least with our given understanding of the economy.

One way forecasters try to look ahead is with the index of leading indicators. A large fall in the leading indicators signals that a recession is likely. Another way of forecasting is with the models of the economy. These models are made up of many equations, each representing a part of the economy.

After making assumptions about the path of the exogenous variables, such as monetary policy, fiscal policy, etc., these models make predictions about unemployment, inflation and other endogenous variables. One must not forget, however, that the validity of these predictions is only as good as the model and the assumptions about the exogenous variables.

Role of Expectation in Policy-Making:

Economics is a young science, and there is still much that, we do not know which suggests that economists should be cautious when advising policymakers. Economists are not completely confident when they make as­sessments about the effects of alternative policies.

Although there are many topics about which knowledge of economists is limited, Lucas has emphasized the question of how people from expectations of the future. Expectations play a crucial role in the economy because they influence the behaviour of consumers, investors, and other economic actors. Expectations depends on many things, including the economic policies been pursued by the government.

Thus, estimating the effect of a policy change requires knowing how people’s expectations will respond to policy change. Lucas has criticised the traditional methods of policy evaluation for not properly taking into consideration this impact of policy on expectation which is known as the Lucas critique.

Active or Passive Role in the Economy:

If the economy has experienced many large shocks to aggregate supply and aggregate demand, and if government policy has successfully insulated the economy from these shocks, then the case for active policy would be clear.

Conversely, if the economy has experienced few large shocks, and if the fluctuations we have observed can be traced to inept economic policy, then the case for passive policy would be clear. Alternatively, our view of stabilization policy should be influenced by whether policy has been historically stabilising or destabilising. Thus, the debate over macroeconomic policy frequently turns into a debate over macroeconomic history.