The following points highlight the top six properties of indifference curve.
Some of the properties are: 1. They Slope Negatively or Slope Downwards from the Left to the Right 2. They are Convex to the Origin of Axes 3. Every Indifference Curve to the right represents Higher Level of Satisfaction than that of the Proceeding One and Others.
1. They Slope Negatively or Slope Downwards from the Left to the Right:
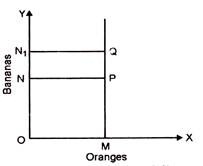
This is an important feature of Indifference Curve. If the total satisfaction is to remain the same, the consumer must part with a diminishing number of bananas as he gets as increasing stock of oranges. The loss of satisfaction to the consumer on account of the downward movement must be made up by the gain through the rightward movement. As such the Indifference Curve must slope downwards to the right.
In this diagram at P, the consumer obtains OM of oranges and ON of bananas. AQ, he gets the same OM. Quantity of oranges, but ON1 of bananas. He secures greater total satisfaction of X than at P. He cannot therefore indifferent between P and Q. Thus it is proved that an Indifference Curve cannot slope upward to the right, nor can it be horizontal or vertical. The only possibility is that it must slope downwards to the right. The consumer will get additional supplies of oranges by sacrificing diminishing quantities of bananas.
2. They are Convex to the Origin of Axes:
ADVERTISEMENTS:
The second property of the Indifference Curve is that they are generally convex to the origin of the axes—the left hand portion is normally steep while the right hand portion is relatively flat. This property of the Indifference Curve is derived from the Law of Diminishing Marginal Rate of Substitution. The marginal rate of substitution neither increases nor does it remain constant.
If the marginal rate of substitution had increased, the Indifference Curve would have been concave to the origin. If the marginal rate of substitution had remained constant, the Indifference Curve would have been a diagonal straight line at 45° angle. The marginal do not rate of substitution increases nor does it remain constant. The marginal rate of substitution on the contrary goes on diminishing. So the Indifference Curve has to be convex to the origin of axes.
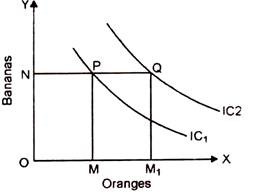
In this diagram, an increase of oranges from OM to OM1 is accompanied by a progressively diminishing number of bananas from ON to ON1. Thus a falling curve whose slope diminishes as we move to the right is bound to be convex to the origin to axes.
3. Every Indifference Curve to the right represents Higher Level of Satisfaction than that of the Proceeding One:
ADVERTISEMENTS:
Let us take two Indifference Curves IC1 and IC2 lying to the right of IC1. At the point P the consumer gets OM of oranges and ON of bananas. At the point Q though the number of bananas remains the same i.e., ON, yet the number of oranges increases from OM to OM1. The total satisfaction of the consumer is therefore bound to be greater at Q than at P.
Hence Q represents a more valued and preferred combination of oranges and bananas than P. As all the points on one Indifference Curve represents equal satisfaction, therefore every point on IC2 represents a combination, preferred to that represented by any point on IC. An Indifference Curve to the right represents a preferred position and therefore a consumer will always try to move on the indifference map as much to the right as possible.
4. Indifference Curves can neither touch nor Intersect each other, so that one Indifference Curve Passes through only one Point on an Indifference Map:
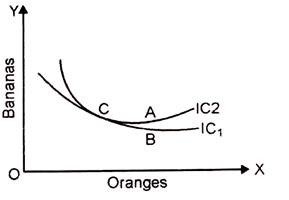
The fourth property of Indifference Curve is that no two Indifference V’ Curves can ever cut each other.
Since point A is an Indifference Curve IC2, it represents a higher level of satisfaction to the consumer c than point B which is located on the lower Indifference c Curve IC1. Point C, however lies on both the curves. This m means that two levels of satisfaction, A and B which are by definition unequal manage to become equal at the point C. This is clearly impossible.
Indifference Curve can never intersect each other:
5. Indifference Curves are not Necessarily Parallel to each other. Although, they are Falling and Negatively Inclined to the Right:
Yet the rate of the fall will not be the same for all Indifference Curves.
This is due to two reasons:
Firstly, the Indifference Curves are not based on the cardinal measurability of utility. Secondly, the rate of substitution between the two commodities need not be the same in all the indifference schedules. It is therefore not necessary that the Indifference Curves should be parallel to each other.
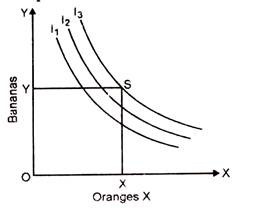
6. In reality, Indifference Curves are like Bangles:
But as a matter of principle their effective region is in the form of segments. This is so because Indifference Curves are assumed to be negatively sloping and convex to the origin. An individual can move to the higher indifference. Curves I2 and I3, until he reaches the saturation upon S where his total utility is the maximum. If the consumer increases his consumption beyond X and Y his total utility will fall.