In this article we will discuss about the factor-intensity reversal of commodities.
The Hecksher-Ohlin theorem rests upon the assumption that the production functions are different for different commodities but these are identical for each commodity in the two countries. Suppose there are two commodities steel and cloth. Steel is capital-intensive (high capital-labour ratio) and cloth is labour-intensive (low capital-labour ratio).
But steel remains capital-intensive in both the countries and cloth remains labour-intensive in both the countries. If this assumption is not fulfilled and the same commodity is capital-intensive in one country and the labour-intensive in the other, the H-O theory breaks down and Leontief paradox can apply to one of the two countries.
The existence of factor-intensity reversal and its cause can be explained in terms of the concept of elasticity of substitution between the two factors— capital and labour. The elasticity of substitution describes the responsiveness of capital-labour ratio (K/L) to the changes in the marginal rate of substitution (MRS) between them.
ADVERTISEMENTS:
ES = [d(K/L)/(K/L)] . [(MRS)/d(MRS)]
Here ES is the elasticity of substitution.
The factor-intensity reversal is likely to take place if the difference in the elasticity of substitution of L and K is greater in the production of two commodities, steel and cloth. If country A is labour- abundant and its wage rate is low, it will produce cloth through labour-intensive techniques. Country B, which is capital-abundant and the wage rate of which is higher, will produce cloth with the capital- intensive technique.
Such a situation will exist if the elasticity of substitution of labour for capital is greater. If at the same time, elasticity of substitution of L for K is low in the production of steel, the two countries will use similar techniques in producing steel, even though their factor prices differ.
ADVERTISEMENTS:
In this situation, there is reversal of factor intensity as cloth is labour-intensive commodity in country A but capital-intensive commodity in country B. Similarly steel is labour-intensive commodity in country A but capital-intensive in country B.
If the factor-intensity reversal exists, the H-O theory breaks down because country A would export cloth—its labour-intensive product and country B would also export cloth which is its capital-intensive product. Since the two countries cannot possibly export the same homogeneous product to each other, the H-O theory does not remain valid.
It is specified above that the greater difference in Es of L for K in the production of two commodities results in factor-intensity reversal. A higher Es of L for K in the case of cloth signifies that the curvature of the isoquant related to cloth C is smaller. On the opposite, a lower Es of L for K in the case of steel implies that the curvature of the isoquant related to steel is greater.
When there is a greater difference in the Es of L for K in the production of two commodities, it can lead to situations in which the isoquants related to two commodities will either be tangent or they will intersect each other. The tangency or sitting over of isoquants and their intersection at more than one points can explain the possibilities of factor-intensity reversal.
ADVERTISEMENTS:
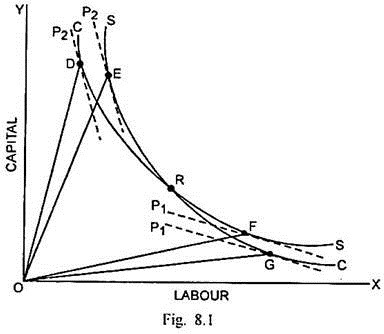
The possibility of factor-intensity reversal, when the isoquant CC of cloth sits over the isoquant SS of steel, can be discussed through Fig. 8.1. In Fig. 8.1, P1 represents the factor-price line of country A and P2 is the factor-price line of country B. Greater steepness of P2 than P1 indicates that country B is capital-abundant while country A is labour-abundant.
In country A, the tangency between the factor price line P1 and CC takes place at G and between P1 and SS at F. The slopes of the factor price lines are the same and they run parallel because they pertain to the same country. So production of cloth and steel takes place in country A at G and F respectively.
K-L Ratio at G = Slope of Line OG
K-L Ratio at F = Slope of Line OF
Since OF is more steep than OG, cloth is more labour-intensive and steel is more capital-intensive in country A.
In country B, given the factor price line P2, the production of cloth takes place at D and that of steel at E. P2 has the same slope in both the cases.
ADVERTISEMENTS:
K-L Ratio at D = Slope of Line OD
K-L Ratio at E = Slope of Line OE
Since OD is steeper than OE, K-L ratio is higher in cloth than in steel. It means the cloth is more capital-intensive than steel in the capital- abundant country B. This clearly reflects factor- intensity reversal. Now labour-abundant country A will attempt to export its labour-intensive product cloth to B and the latter will attempt to export its capital-intensive product cloth to A and consequently H-O theory stands refuted.
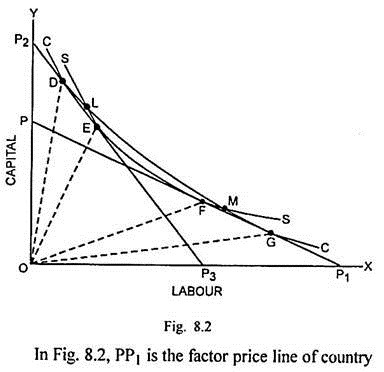
The factor-intensity reversal can exist also when the isoquants related to two commodities intersect each other at more than one point. This is shown through Fig. 8.2.
ADVERTISEMENTS:
A and P2P3 is the factor price line of country B. The less steepness of PP1 than P2P3 signifies that country A is labour-abundant while the country B is capital-abundant. CC is the isoquant related to cloth and SS is the isoquant related to steel. The two isoquants have different curvatures and intersection between them takes place at points L and M. The factor-intensity reversal occurs to the right of point M and to the left of L.
The capital-intensities of two products in the two countries can be measured as below:
ADVERTISEMENTS:
K-L Ratio in cloth at G = Slope of Line OG
K-L Ratio in steel at F = Slope of Line OF
K-L Ratio in cloth at D = Slope of Line OD
K-L Ratio in steel at E = Slope of Line OE
Since slope of OG is less than the slope OF, capital-intensity of steel is more than the capital- intensity of cloth in country A. On the other hand, since slope of OD is more than the slope of OE, capital-intensity of cloth is greater than the capital- intensity of steel in country B. This again reflects the existence of factor-intensity reversal.
ADVERTISEMENTS:
Country A will attempt to export its labour-intensive product cloth to B, whereas the latter will attempt to export its capital-intensive product cloth to the former. Since both cannot possibly export the same homogenous commodity cloth, the H-O theory stands invalidated.
It is, of course, true that factor-intensity reversal has a very damaging implication for the Heckscher- Ohlin theory. The most pertinent question is related to the extent to which the factor-intensity reversal is prevalent in the real life.
The economists relied mostly upon the Cobb- Douglas production function in their investigations up to 1961. Since the production function took the Es = 1 in the production of all the commodities, it was considered unsuitable to measure the extent of factor-intensity reversal.
After the development of Constant Elasticity of Substitution (CES) production function by Arrow, Chenery, Minhas and Solow, Minhas attempted to employ this production function for measuring the reversal of factor-intensity in 1962. He made use of the comparative data for 19 industries and found factor-intensity reversal in 5 cases. It led to the conclusion that the factor- intensity reversal was fairly present.
The finding of Minhas was refuted by Leontief in his 1964 study based on 21 industries. He found the factor reversal occurred in only 8 percent of the cases. When two natural resource intensive industries were removed out of them, the factor- intensity reversal fell down to 1 percent of the cases. This led Leontief to conclude that factor- intensity reversal was a rare occurrence and therefore, H-O model remains valid.
Minhas attempted another study based on 20 industries in the United States and Japan. He computed K-L ratio for these industries and ranked them according to the K-L ratio in each country. He found the rank correlation co-efficient in the capital-intensities in industries in the two countries as +0.328 and concluded that the factor-intensity reversal was fairly common.
ADVERTISEMENTS:
D.P.S. Ball, however, pointed out that the exclusion of agriculture and two natural resource industries resulted in a steep rise in rank correlation to 0.77. It implied that the factor-intensity reversal was not a common phenomenon. Moroney also refuted Minhas’ findings and remarked that factor-intensity reversal “has much less empirical importance than theoretical interest. In a 1968 study, Hal Lary, on the basis of data concerning 13 main groups for 9 countries, tended to reject the reversibility hypothesis.
From the above account, it becomes clear that the overwhelming evidence is against the factor- intensity reversal. Consequently, the H-O theory need not be rejected on this ground.