The Neo-classical Theory of Investment (With Diagram)

Let us make an in-depth study of the Neo-Classical Theory of Investment.

The modern approach to business investment is based on Dale Jorgenson’s approach known as the neo-classical theory of investment.

Jorgenson’s theory provides the micro- foundation of the aggregate investment function.

For analytical convenience, we classify an economy’s firms into two broad categories, viz., (i) production firms that produce goods and services using capital owned by other firms by paying lease rental and (ii) rental firms, which buy capital and lease (rent) it to the producing units.

The Rental Price of Capital:

The focus of attention in Jorgenson’s theory is on the typical production firm. The firm, operating in a pure competitive model, is guided by the neo-classical marginalist rule of profit maximisation. The key concept in the neo-classical theory is the rental price of capital.

A profit-seeking firm compares the cost and benefit of each unit of capital while taking decision on how much of capital to lease in by paying a fixed rental per period. Let us, for instance, take the case of a construction company which has got the contract to construct a multi- storeyed building within a year’s time. It requires an earth-moving equipment for three months.

There is no point in buying this machine at a high cost. It gains by hiring this machine from another company (the rental firm) by paying a lease rental. The rental price of capital is the periodic payment that has to be made by the construction company to the leasing firm (which specialises in leasing out the machine) for a certain period to hire the earthmoving equipment.

The construction company obtains the equipment by paying a rental of R per period and it sells its output at a price of P. So the real cost of a unit of capital to the production firm is R/P. The real benefit of a unit of capital to a producing firm is its marginal product. The marginal product of capital (MPK) is the addition made to the total product of the firm by one extra unit of real capital.

So long as the MPK exceeds the rental price of capital, a firm makes extra profit by hiring and using an extra unit of capital. However, as more and more capital is used, MPK falls and a production firm maximises profit by equating MPK with the real rental price. In other words, a profit-maximising firm takes capital on lease rental basis until the MPK falls to equal the real rental price.

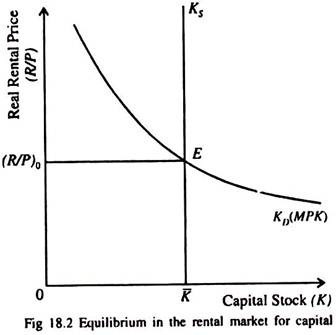
Fig. 18.2 shows the equilibrium in the rental market for capital. The demand curve of capital is the MPK curve. It slopes down­ward from left to right because as more and more units of capital are used, MPK falls. In other words, MPK is low when the level of capital is high. The aggregate supply of real capital remains fixed in the short run.

So the supply curve of capital (indicating the amount of capital avail­able in the economy per period) is a vertical straight line. The real rental price of capital is (R/P)₀. This is indeed the equilibrium rental price because it is the rate which brings the demand for capital (as determined by MPK) in line with the fixed supply.

The Cost of Capital and its Determinants:

The benefit of the rental firm from owning capital is the revenue it gets from renting it to the production firms. It receives the real rental price of capital (R/P) for each unit of capital it owns and rents out.

There are three types of costs of owning and renting out a unit of capital:

1. Interest on loan:

When a rental firm borrows funds to buy a unit of capital for the purpose of renting it out, it has to pay interest on the loan. The interest cost is iP_K where i is the nominal interest rate and P_K is the purchase price of a unit of capital.

2. Capital loss:

It is quite possible for the price of capital (the firm is renting out) to fall, in which case the rental firm loses. The reason is that the market value of the firm’s capital usually falls. The cost of this loss is -ΔP_K.

3. Depreciation:

The rate of depreciation of capital is another component of the cost of owning and renting out real capital. The rate of depreciation (d) is measured by the proportion of value of the capital lost per period due to wear and tear, i.e., dP_K.

So the total cost of renting out a unit of capital for one period is thus:

Cost of capital = iP_K – ΔP_K + dP_K = P_K(i – ΔP_K/P_K + d) … (1)

So there are four determinants of cost of capital, viz., P_K, i, the rate at which P_K is changing and d. We put a negative sign before ΔP_K/P_K because P_K is assumed to be falling.

If we make the assumption that the price of capital goods rises with the prices of other goods, as is the case during inflation, then (ΔP_k/P_k) is interpreted as the overall rate of inflation (π). Since the real rate of interest (r) is the nominal rate of interest (i) less the rate of inflation (π), the cost of capital (C_K) is

C_K = P_K(i – π + d) = P_K(r + d) … (2)

So there are three determinants of the cost of capital, viz., P_K, r and d.

The real cost of capital (C_r) is expressed as

C_r = (P_K/P) (r + d) … (3)

where P is the overall price index. It is the weighted average of all prices. Equation (3) expresses the cost of capital relative to the prices of other goods in the economy. The real cost of capital is the cost of acquiring and leasing out a unit of capital measured in units of real GDP and has three determinants — P_K/P, the relative price of capital goods, r and d.

The Determinants of Investment:

Since all economic decisions are taken at the margin, a rental firm, whose objective is profit maximisation, has to take decisions regarding whether to increase or decrease its capital stock on the basis of its own benefit-cost calculations. By renting out each unit of capital, the firm earns revenue (R/P) and incurs the real cost (P_K/P) (r + d). So its real profit per unit of capital or the rate of profit is

p = (R/P) – (P_K/P) (r + d) … (4)

Rate of profit = Real revenue from capital – real cost of capital.

Since the real rental price of capital equals the MPK, in equilibrium, the rate of profit may be expressed as:

p = MPK – (P_K/P) (r + d) … (5)

The rental firm makes a profit (i.e., p > 0) if MPK exceeds the real cost of capital. The converse is also true.

Net investment refers to the absolute change in the capital stock of a firm (I = ΔK = K_t – K_t-1,). Equation (5) suggests that investment decision of the rental firm, i.e., decision regarding whether to add to its capital stock or allow it to wear out completely depends on whether owning and leasing out capital is a profitable proposition.

So long as MPK exceeds (P_K/P) (r + d), the rental firm finds it profitable to make net investment, i.e., add to its existing stock of capital. The converse is also true. If MPK is less than (P_K/P) (r + d) the firm will not care about even its existing stock of capital and just allow it to depreciate and shrink.

The Investment Function:

What is true of a firm which owns and rents out capital is equally true of a firm which both uses and owns capital. So we can write

ΔK = I_n[MPK – (P_K/P) (r + d)] … (6)

where I_n depends on or is a function of the difference between the MPK and the real cost of capital (C_r). This difference shows how much net investment responds to the incentive to invest. There is an incentive to invest if MPK > (P_K/P) (r + d).

The investment function is

I = I_n[MPK – (P_K/P) (r + d)] + dK … (7)

where I is gross investment which is equal to net investment l_n plus depreciation dK. Thus total spending on business fixed investment depends on MPK, the real cost of capital and the amount of depreciation (i.e., the rate of depreciation times the amount of capital).

Shift of the Investment Schedule:

Any favourable development in the economy which raises the MPK increases the profitability of investment and causes the investment schedule I of Fig. 18.3(b) to shift to the right to I’. This means that more investment takes place at the same real rate of interest.

For example, a favourable technological change which raises the MPK increases the amount of capital goods that lease-renting firms desire to buy at the same real rate of interest.

Intertemporal Adjustment of Capital Stock:

If MPK is initially above the real cost of capital, the capital stock will rise and the MPK will fall. If MPK is initially below the real cost of capital, the capital stock will fall and MPK will rise.

So, ultimately, as the economy’s capital stock adjusts, the MPK approaches the real cost of capital and the steady-state level of capital is expressed as:

MPK = (P_K/P) (r + d)

Since in such a situation total profit from capital is maximum (constant) and marginal profit is zero, no addition is made to society’s stock of capital, i.e.,

ΔK = I = 0

because MPK – (P_K/P) (r + d) = 0. So there is no incentive to make further investment in fixed capital. Thus in the long run when the adjustment of capital stock continues over time MPK equals the real cost of capital. The speed of adjustment toward the steady state depends on the speed with which firms adjust their capital stock. This, in its turn, depends on the cost of building, delivering and installing new capital.