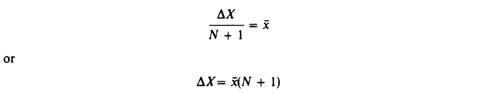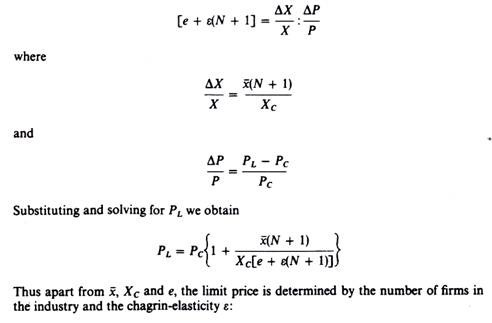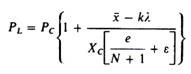Bhagwati extended Modigliani’s model in two directions. Firstly, he incorporated two additional determinants of the limit price in Modigliani’s expression.
Secondly, he introduced a term which renders the limit-price theory dynamic, in the sense that it can predict the changes in the limit price arising from a growing market.
The two factors which Bhagwati introduced into Modigliani’s model are the number of firms in the industry and a measure of the switch of customers of established firms to the entrant due to their feeling of dissatisfaction (chagrin) from their exploitation by the suppliers charging them a higher price (before entry occurred). Regarding the number of firms Bhagwati assumes that, as price falls with entry, some of the new buyers will buy from established firms whose name is known, and some will buy from the entrant.
For simplicity Bhagwati assumes that the increment in the market demand is shared equally between the established firms and the entrant:
The ‘chagrin effect’ is a positive elasticity which measures the proportionate decrease in the sales of established firms as the price decreases and dissatisfied customers turn to the new entrant. It is denoted by e and is of opposite sign to the normal price elasticity e. Thus the relevant elasticity for the determination of the limit price by the established firms is (approximately)
The premium obtainable in an industry will vary directly with:
(1) The minimum size of scale of most efficient production (x) and
ADVERTISEMENTS:
(2) The number of existing firms (N); and inversely with (1) the size of the total market (Xc), (2) the price-elasticity of industry demand and (3) the extent to which existing buyers will transfer custom to the entrant consequent upon entry. (Bhagwati, ‘Oligopoly Theory, Entry-Prevention and Growth’.)
The above expression has been extended to cover dynamic changes in market demand. If demand increases by an amount λ and out of this increase k per cent accrues to the new entrant, the limit price will be defined by
where Xc is now the aggregate demand at the competitive price after growth. The factor k is inversely related to PL, denoting the fact that entry is easier in an expanding market. The faster the growth in demand the smaller the premium by which PL will exceed Pc.
ADVERTISEMENTS:
The important implication of this formulation is that if (kλ) > x, the prevention of entry is impossible, since PL must fall below Pc, that is, to a level that does not cover the LAC. This cannot be a long-run equilibrium situation. So, the use of price policy to prevent entry becomes an ineffective device. Under these conditions the only entry- preventing policy must be based on other actions such as keeping adequate spare capacity continuously so as to keep production at the same pace as demand.
This, however, may be a costly and non-profitable policy. Furthermore it requires a good forecasting ability on the part of the entrepreneur. If (kλ) > x, that is, if the market is growing very fast, the existing firms cannot rely on price alone as the appropriate instrument for their entry-forestalling policy.
They must look for methods to ensure the maximum appropriation to themselves (rather than to any potential entrant) of the increment of the growing demand. Thus, in dynamic markets, if the firms want to prevent entry they must look for the factors that determine their share and try to operate on those factors that are under their control.
The theoretical problem thus shifts from devising an entry-preventing price to a formal analysis of the non-price factors which determine the share of the existing firms in the growing market and the ways in which these are within the range of influence of these firms. (Bhagwati, ‘Oligopoly Theory, Entry-Prevention and Growth’.)