Market Equilibrium in the Marshallian Sense | Microeconomics

In this article we will discuss about the market equilibrium in the Marshallian sense.

Suppose, the demand and supply functions for a commodity are:

q^d = φ(p^d)                                           (4.18)

and q^s = Ψ(p^s)                                   (4.19)

where p^d and p^s denote the demand price and supply price, respectively. It can be called the inverse of the demand and supply functions (4.18) and (4.19) the demand and supply curves.

Therefore, the equations of these curves would be:

p^d = φ⁻¹(q^d)                                     (4.20)

and p^s = Ψ⁻¹(q^s)                            (4.21)

Now define the excess demand price, F(q), as the difference between the demand price (p^d) and the supply price (p^s) at any q.

it can be written, therefore:

F(q) = p^d−p^s

= φ^-1(q^d) − Ψ^-1(q^s)                        (4.22)

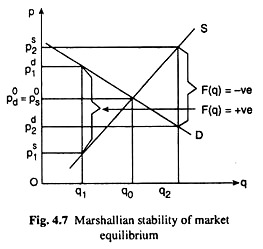
The excess demand price F(q) may be positive or negative according as p^d > p^s or p^s > p^d. For exam­ple, in Fig. 4.7, at q = q₁, F(q) = p₁^d − p₁^s is posi­tive and, at q = q₂, F(q) = p₂^d – p₂^s is negative. The market is in equilibrium if at some q, p^d = p^s and F(q) = 0.

This has happened at q = q₀ in Fig. 4.7. On the other hand, the market is not in equilibrium at any q if F(q) ≶ 0. For example, at q = q₁ and at q = q₂, F(q) is positive and negative respectively, and at both these quantities the market is not in equilibrium.

Marshallian Stability Condition:

The Marshallian stability condition is based on the behaviour assumption that producers will raise their output when F(q) > 0, i.e., when at output q, the buyers are offering a higher price than what the sellers are demanding (p^d > p^s), and the producers will lower their output when F(q) < 0, i.e., when at output q, the buyers are offering a price which is smaller than what the sellers are demanding (p^d < p^s).

Given this behaviour assumption, the market will be stable in the Marshallian sense if

i.e., if there is an inverse relation between q and F(q).

The logic behind the Marshallian stability condition (4.23) is this:

If F(q) is positive, the producers will raise their output (q) and as q rises F(q) would have to decrease, and, eventually, it would have to decrease to zero where the market equilibrium, again, would be restored.

On the other hand, if F(q) is negative, the producers will lower their output (q), and, as q decreases, F(q) would have to increase, and eventually, F(q) would have to be zero, where the market would again reach equilibrium. From (4.23),

Equations (4.23) and (4.24) give us the market stability condition in the Marshallian sense.

It is evident from (4.24) that the market would be stable if:

(i) The demand curve is negatively sloped and the supply curve is positively sloped.

(ii) The demand curve is flatter than the supply curve when both these curves are positively sloped.

(iii) The numerical slope of the demand curve is larger than that of the supply curve, i.e., the demand curve is steeper than the supply curve, when both these curves are negatively sloped.

On the basis of our analysis of the market stability conditions of Walras and Marshall, It may be concluded that if the demand curve is negatively sloped and the supply curve is positively sloped, then the market would be stable in both the Walrasian and the Marshallian sense. But if both these curves are positively or negatively sloped, the requirements of Walrasian and Marshallian stability are just the opposite of each other.