Mean Deviation: Coefficient of Mean Deviation

Introduction:

In Range, we calculate it by taking the upper and lower most limits; while calculating Percentile Range, also two terms are taken lying between and P₁₀ and P₉₀.

Similarly in case of Quartile Deviation we take terms belonging to Q₁and Q₃ e.g. 25% lower and 25% upper terms are left out.

In all these cases, there is a single, but very big drawback. It takes only two terms in calculations and all other data is ignored. So only two terms from the whole data cannot give the clear picture of the whole. Sometimes we get Range, Percentile Range and Quartile Deviation identical for a series but their composition may be much different from each other.

We thus need an ideal measure of dispersion, which takes all the terms of the series for calculation and be calculated from an Average. Such measures which are calculated from average are known as ‘Average Deviation’.

“Average deviation is the average amount of scatter of the items in a distribution from either the mean or the median, ignoring the signs of the deviation. The average that is taken of the scatter is an arithmetic mean, which account for the fact that this measure is often called the mean-deviation”. —Clark and Schkade

Mean deviation or average deviation is the average difference between the items in a series from the mean or median or mode. Theoretically, it is beneficial to take deviations from median. It is because the sum of deviations of terms from median is minimum when ± signs are ignored.

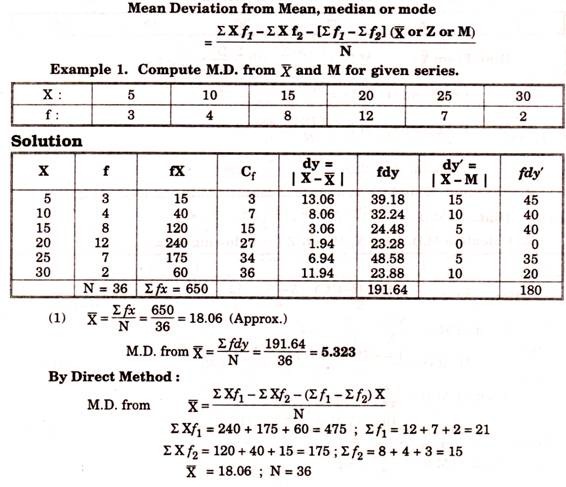
The formula for calculating mean deviation is

M.D. = Σf|D|/N; where M.D. = Mean Deviation

f is frequency of corresponding interval, N is total no. of frequencies (Σf)

I DI read as Mod D = (X-A) is the modulus value or absolute value i.e., deviations from median or mean or mode ignoring ± signs.

Coefficient of Mean Deviation:

It is calculated to compare the data of two series. The coefficient of mean deviation is calcvilated by dividing mean deviation by the average. If deviations are taken from mean, we divide it by mean, if the deviations are taken from median, then it is divided by mode and if the “deviations are taken from median, then we divide mean deviation by median.

B. For Discrete Series:

M.D. = ∑fdy/N; Where; N=∑f

And dy is the deviation of variable from X, M or Z ignoring signs (Taking +ive signs only).

Steps to Calculate:

1. Take X, M or Z series as desired.

2. Take deviations ignoring signs.

3. Multiply dy by respective f; get ∑fdy

4. Use the following formula

M.D. = ∑fdy/N

(Note : If value of X or M or Z is in decimal fractions better use Direct Method to get result easily)

When Mean or Median or Mode is in Fractions, in that case, Direct formula is applied

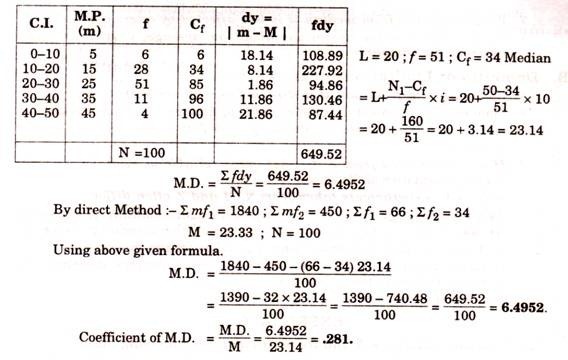
C. For Continuous Series:

For Continuous Series also ; M.D. = ∑fdy/N

Important Note:

Whenever asked to find x and M.D. from x i It is useful to use direct method to find X as well as mean deviation. As in Exp. 4 ; we get X = ∑fm/N = 2290/100 = 22.9. We need not go through columns dx, fdx, dy and fdy in this question.