Monopoly Equilibrium (With Diagram)| Markets

The profit maximising hypothesis can no longer be considered as an appropriate one to explain the behaviour of the firm for the following reasons:

First, it may be pointed out that in deciding about his price-output policy, the entrepreneur does not aim at maximising his profit at a particular time or for a particular period of time. Instead, he tries to have a steady flow of profits for a long time. In other words, he is actuated by the desire for secure profit.

According to Prof. Rothschild, profit maximising is valid for explaining the behaviour of a firm which is working under conditions of perfect competition or monopolistic competition with a large number of firms or when a firm enjoys absolute monopoly because, in these cases, the problem of security does not arise.

But, Prof. Rothschild points out that, in the field of oligopoly, the profit maximisation as­sumption is no longer sufficient.

In this field, there is the desire for achieving a secure position as well as the power to act on this desire. Prof. Baumol has also challenged the assumption of profit maximisation. He has argued that maximisation of sales (revenue) rather than of profits is the ultimate objective of the firm.

He says that the firm tries to promote sales not merely as a means to further its other objectives, viz., operational efficiency and profits, but, for a businessman, sales have become an end in itself. He therefore, thinks that sales-maximisation is the most valid assumption about the be­haviour of the firm.

Prof. Baumol points out, however, that in their attempt to promote sales, businessmen do not completely disregard costs incurred on output, and profits to be made. He also concedes that there is some conflict between the firm’s sales goal and its profit objective.

He points out that, in the actual world, businessmen usually promote sales subject to the limitation that costs incurred are covered plus a usual rate of return on investment is obtained. Thus, what we see is that the whole concept of rationality has undergone a change these days. Rationality is implicit in profit maximisation but rational behaviour need not necessarily be profit-maximising.

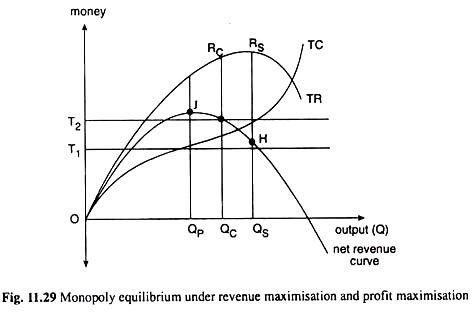
So, we can suggest Prof. Baumol’s sales (or revenue) maximisation hypothesis subject to a profit constraint as an alternative to the hypothesis of profit maximisation. This hypothesis can be illustrated with the help of Fig. 11.29.

In this figure, TR and TC are the total revenue and total cost curves. Net revenue or profit at each output is the difference between TR and TC, and it is given by the net revenue curve. There will normally be a well-determined output level that maximises sales in terms of money, or revenue.

This level can ordinarily be fixed with the aid of the well-known rule that maximum revenue will be obtained only at an output at which the elasticity of demand is unity, i.e., at which marginal revenue is zero. In Fig. 11.29, this output is OQ_s.

But this rule does not take into account the profit constraint. That is, if at the revenue or sales maximising output (OQ_s) the firm does, in fact, earn enough or more than enough profits to keep its stockholders satisfied, then it would produce the sales-maximising quantity.

In this case, the profit constraint does not act as an effective barrier to sales maximisation. But if at this output (OQs), the profits are too low, the firm’s output must be changed to a level which, though it fails to maximise sales, does meet the profit requirements.

We see then that two types of equilibrium appear to be possible. One in which the profit constraint does not act as an effective barrier to sales maximisation, and one in which it does.

In Fig. 11.29, the profit and sales maximising output are OQ_P and OQ_s respectively. Now, if the minimum required profit level is OT₁, for example, then the sales-maximising output OQ_s will provide plenty of profit (= HQ_S > OT₁) and the sales maximiser will produce an output of OQ_s.

His selling price will then be Q_sR_s/OQ_s. But if the producer’s minimum required profit level is OT₂ (OT₂ > HQ_S), the output OQ_s that yields insufficient profit now (HQ_S < OT₂) will clearly not do. Instead, his output will be reduced to OQ_c, which is just compatible with his profit constraint.

The profit-maximising output OQ_P will usually be smaller than the one (OQ_c or OQ_s) which yields either type of sales maximum. This is because at the point of maximum profit we have MR = MC. Since MC is normally positive, MR is also positive, and so a further increase in output will increase total sales.

Therefore, if at the point of maximum profit, the firm earns more profit than the required minimum, as it does in Fig. 11.29 (since JQ_P > OT₂), then it will pay the sales maximiser to lower his price and increase his physical output.