Pricing of Product under Natural Monopoly | Markets

In this article we will discuss about the pricing of a product under natural monopoly with its problems.

There are many production processes where average cost of production declines over the entire range of market demand (as in Fig. 11.26) because of economies of scale. This implies that one firm can satisfy the entire market demand more cheaply than a multiple of firms could.

That is why it is thought that monopoly may arise naturally in these production processes. Such a monopoly is called a natural monopoly. Virtually, all public utilities are natural monopolies.

Municipal waterworks, electrical power companies, telephone companies, transportation serv­ices are examples of the production processes which may be organised as natural monopolies. We shall see that if a natural monopoly is not regulated, if it is left free to make its own profit-maximising price-output policy, then the inefficiency of monopoly would be too much for the society to accept.

In other words, principle of profit maximisation would not be able to prop­erly utilise the economies of scale that give rise to a natural monopoly, and society would be the loser. That is why a natural monopoly needs to be regulated.

An alternative to regulate natural monopoly is to let the government operate it. If the gov­ernment operates a natural monopoly, then ideally it should follow the p = MC principle and pay a lump-sum subsidy to keep the firm in operation.

By doing this, the government would cause the output of the firm to rise and price to fall which would often be a greater gain to the society than the loss involved in the payment of subsidy.

Lastly, it should be mentioned that the government would have to set up an effective machin­ery that would correctly measure the average cost of the firm so that price can be appropriately set when the p = AC principle is followed. Also, the machinery should be given a freehand to deter­mine the quantum of subsidy that should be paid when the p = MC principle is put into practice.

Problem of Pricing under Natural Monopoly:

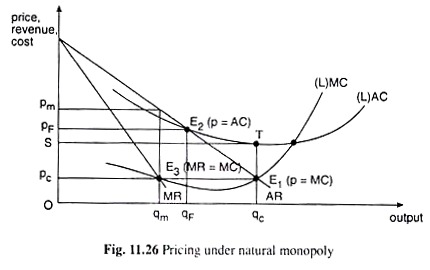
We shall discuss the problem of pricing the product of a natural monopoly with the help of Fig. 11.26. In this figure, we have shown the AR, MR, AC and MC curves of the monopolist. The Pareto-efficient output of a firm is one at which price is equal to marginal cost (p = MC). For here the money that the buyer is willing to pay for the marginal unit is equal to the additional cost for that unit.

In Fig. 11.26, we may compare between the points E₁, E₂ and E₃ that are, respectively, the p = MC, or, competitive solution, the p = AC, or, the average cost pricing solution and the MR = MC, or, the monopoly profit-maximising solution. Of these three solutions, the first one is the most efficient (i.e., the Pareto-efficient) solution; here, output, q_c = Oq_c, is the largest, and the price, p_c = Op_c, is the smallest.

On the other hand, the monopoly profit-maximising solution at the point E₃ is the worst, for here the output, q_m = Oq_m, is the smallest and the price, p_m = Op_m, is the largest. On his own, the monopolist would want to stick to this MR = MC solution for this would enable him to achieve profit maximisation.

But from the point of view of society, the owner of a natural monopoly cannot be allowed to enjoy this solution. That is why natural monopolies are regulated or operated by the government.

It may follow from above that a monopoly is best regulated if it is made to accept the competitive or p = MC solution which is also Pareto-efficient. However, a natural monopoly by definition suffers from insufficiency of demand relative to its productive capacity.

It is assumed that the demand curve of the firm under such a monopoly passes through its AC curve to the left of the minimum point of the latter. That is why the p = MC solution under natural monopoly would result in AR being less than AC, i.e., the firm here would suffer from loss or a negative economic profit.

In Fig. 11.26, at the p = MC point E₁, the firm’s loss (i.e., TC – TR) would be equal to □STE₁p_c. Therefore, the p = MC solution cannot be a feasible proposition for a natural monopoly unless the authorities are ready to pay reasonable subsidy to the busi­ness.

On the other hand, the regulatory authority would have difficulty in accepting the mo­nopoly solution, MR = MC at the point E₃. Because, here the firm would supply too little at too high a price although it is in a position to produce more under diminishing average cost of production.

We have to examine, therefore, the remaining option, i.e., the p = AC or the full-cost pricing solution. While regulating a natural monopoly, if the authorities do not consider to pay any subsidy to the business, then they must see that the monopoly operates on its average cost curve so that all its costs are recovered, and also on its demand curve so that demand for the product is fully satisfied.

This means that the monopoly should be asked to operate at the point where its AC curve meets its demand (or AR) curve.

This is the p = AC or the full-cost pricing solution. Here the firm would sell its product at a price which is equal to its average cost of production and at the same time the buyers who are willing to pay the price would be able to meet their demand fully.

That is why the p = AC solution is often considered to be a reasonable price policy for a natural monopoly, although output here would be lower than the efficient level (i.e., the p = MC level) and price would be higher than this level. In Fig. 11.26, the p = AC solution is given at the point E₂. At this point, output is q_F < q_c and the price is p_F > p_c.