When does the Profit of a Firm become Maximum? | Economics

In this article we will discuss when does the profit of a firm become maximum. Also learn about why is the equality of marginal revenue and marginal cost essential for profit maximisation in all types of markets.

The basic objective of a firm under all types of market situation is the profit maximisation. Accordingly, a firm, whether competitive or mo­nopolistic, must seek out the equilibrium price and quantity, which gives it the’ largest profits.

Such an equilibrium price and quantity of a firm can be determined in two ways:

The Largest Difference between Total Revenue (TR) and Total Cost (TC):

The simplest way to find out the maximum total profits of a firm is to make a comparison between its revenue and costs. Firstly, we must know much revenue the firm earns from selling different units of its product. Then, we have to find out how much it costs to produce the same units.

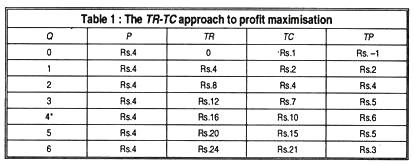
In other words, we must know the total revenue (TR) and the total cost (TC) at different levels of output. Total profit (TP) of a firm equals total revenue minus total cost: TP=TR-TC=P x Q-TC. To maximise its profits the firm must find out the optimal price and quantity, that gives the largest difference, TR-TC. This is shown in Table 1.

Table 1 shows that the output of 4 units gives the firm maximum total profits, i.e., Rs. 6. The price or average revenue is assumed to remain constant at Rs. 4 at all units of output as happens under perfect competi­tion. So, the firm would produce 4 units of output at the price of Rs. 4 per unit.

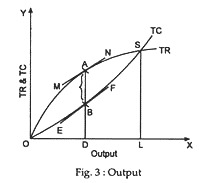
The TR-TC approach is shown graphically in Fig. 3 where the TR curve shows the total receipts from various units of output and the TC curve indicates the total cost of pro­ducing the same units. It is obvious that the largest profit which the firm can make will be earned when the vertical distance between TR and TC curves is maximum.

This is attained at the output level at which the slopes of the two curves are the same, that is, where the tangents MN and EF to the revenue and cost curves, respectively, are parallel. The figure shows that at the output level OQ the said vertical distance (AB) is the maximum, because here they said two tangents are parallel.

The Equality between Marginal Revenue (MR) and Marginal Cost (MC):

The second way of discovering the optimal quantity and price is to make a comparison between the marginal revenue and the marginal cost at different levels of output. Marginal cost is the extra cost of producing one extra unit of output. Similarly, marginal revenue is the extra revenue obtained from the sale of one additional unit of output.

To find out the maximum total profits a firm is’ to compare its MR with MC. So long MR>MC a firm can increase its total profit by producing more and more units. But when MC < MR, the firm incurs losses and so it will reduce its output level. Logically it follows then that the total profit of a firm become the maximum at the output level at which MC=MR, in which case the extra cost balances extra revenue.

This is so because when MR=MC, a firm’s marginal profit is zero when its total profit is maximum (constant). When this happens, it is not possible to make any extra profit by producing and selling any extra unit of output. So, a firm maximises when by producing and selling the extra unit it adds as much as to revenue as to the cost.

The addition to revenue is marginal revenue and the addition to cost is marginal cost. Therefore, MR=MC is the condition of maximum profit. But the equal­ity of MR with MC is a necessary and not a sufficient condition of profit maximisation. The sufficient condition is that the MC curve intersects the MR curve from below and not from above. So, a firm increases its total profit by expanding its output so long MR>MC, and because of losses it reduces its output when MC<MR.

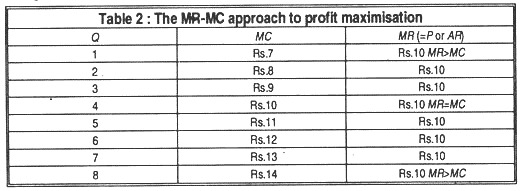
This point is illustrated in Table 2 (under a competitive situation):

Table 2 shows that up to 3 units of output MR>MC; so the firm can increase total profit by producing and selling more units. But, from 5 units onwards MR<MC; so the firm will reduce its output level. But, at 4 units of output MR is exactly equal to MC; so a profit-seeking firm will produce 4 units at constant MR of Rs. 10 (as happens under perfect competition) because in such a situation its total profits are maximum. The firm will be in equilibrium when it produces 4 units at the price of Rs.10 per unit.

The same can be shown with the help of the following mathematical calculation:

Let us take π = total profit

TR = total revenue

TC = total cost

d = differential (small increase or decrease)

Q = quantity produced or sold.

We know: π = TR – TC

Or, dπ/dQ = dTR/dQ = dTC/dQ

But, total profit is maximum when marginal profit is zero or when

Dπ/dQ = 0

From the above equation then total profit is maximum when

dTR/dQ = dTR/dQ = 0

Or, dTR/dQ = dTC/dD

Here, dTR/dQ is MR, dTC/dQ is MC

Or, MR = MC

It shows that the total profit is maximum when MC = MR.

Conclusion:

These two methods of discovering the optimal position of a firm seeking maximum profits are not, however, different. It can be shown that the difference between TR and TC (i.e., total profit) is maximum at the output level at MC = MR.