The Modern Theory of Rent | Microeconomics

In this article we will discuss about:- 1. Causes for the Emergence of Rent 2. Complete Inelasticity of Supply and Rent 3. Less than Perfect Elasticity of Supply and Rent 4. Infinite or Perfect Elasticity of Supply and Rent 5. Share of Economic Rent in an Input’s Income 6. Definition of an Input and Length of the Time Horizon, and Economic Rent.

Causes for the Emergence of Rent:

David Ricardo has explained in his theory of rent that the main reason behind the emergence of rent of land is the inelasticity in the supply of land. The modern theory of rent has applied that concept in a wider perspective.

The modern theorists were quick to point out that not only land, but also any other factor might have or might develop inelasticity in their supply. Therefore, like land, the other factors also could earn rent

According to the modern theory, land or any other factor of production may earn more than its minimum supply price in its present use, if its supply is less than perfectly elastic, i.e., if its supply is subject to some limitations.

It may be noted that if the supply of a factor of production is indefinitely large at any particular price, i.e., if its supply curve is a horizontal straight line, then we say that the supply of the input is perfectly elastic or the supply is unlimited.

On the other hand, if:

(i) The supply of an input is completely fixed whatever may be its price, and 

(ii) The supply of an input may increase only when its price increases, then we say that the supply of the input is subject to limitations—the supply is less than perfectly elastic.

In the case of:

(i) The supply is completely inelastic (e = 0), and the supply curve would be a vertical straight line, and in the case of

(ii) The elasticity of supply lies between zero and infinity (0 < e < and the supply curve would be upward sloping.

Let us now see what determines the minimum supply price of a factor and how a factor can earn more than its supply price on account of its limited supply. One of the major differences between the Ricardian and modern theories of rent is that the former assumes that land can be used to produce a single agricultural item and it has no alternative use and the latter asserts that land can be put to more than one alternative use.

Now, the maximum amount that any unit of a factor may earn in an alternative use is its minimum supply price in the present employment.

For example, if a worker gets a maximum of Rs 4,000 as his wage in an alternative field, then his minimum supply price would be Rs 4,000 in his present employment, i.e., if he does not get Rs 4,000 as his wage, then he would get transferred to the best alternative use where he would earn at the rate of Rs 4,000 per period. That is why the minimum supply price of a factor (here Rs 4,000) is also called his transfer earning.

Again, if he gets the opportunity of being employed in his present use, he would lose the opportunity of earning Rs 4,000 from the alternative use. That is why it is said that Rs 4,000 is the opportunity cost of his present employment. Therefore, the minimum supply price of a factor is also called its transfer earning or the opportunity cost of its present use.

We shall discuss now how rent emerges in modern theory because of limitations in the supply of a factor.

Complete Inelasticity of Supply and Rent:

If a factor of production is completely specific to its present use, i.e., if it has no alternative use, then its supply in the present use would be completely fixed or completely inelastic (e = 0). Since it has no alternative area of employment, it cannot transfer itself from the alternative field to the present use or from the present use to the alternative use.

In this case, the transfer earn­ing of the input is zero and its minimum sup­ply price in the present use is also zero.

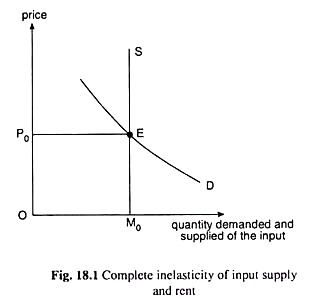
Since supply is completely fixed, the sup­ply curve of the input would be a vertical straight line like the line S in Fig. 18.1. That is, whatever may be the price, its supply would be a constant (= M₀). In Fig. 18.1, the demand curve for the input is D.

This curve will be, as usual, sloping downwards to the right. Now, it is obtained at the point of intersection, E, of the demand and supply curves that a quantity of M₀ of the input is demanded and supplied at the price P₀.

Here, the supply price of each unit of the input is zero and the actual price received by it is P₀. Therefore, the price (P₀), i.e., income of each unit of the input, would all be a surplus over its supply price, and so, the whole of total income received by all the M₀ units of the input would be the total amount of surplus or economic rent that would be earned by all the units taken together.

In Fig. 18.1, the total income received by the M₀ units of the input is P₀ x M₀ = □ OP₀EM₀. On the other hand, the aggregate of minimum supply price of the M₀ units of the input is M₀ x 0 = 0. Therefore, the total amount of economic rent earned by the input is □OP₀EMq – 0 = □OP₀EM₀ = total income received by the input.

Less than Perfect Elasticity of Supply and Rent:

If all the units of an input are homogeneous in a particular use and if the units are not equally efficient in their respective alternative uses, then their earnings in alternative uses would not be equal, and then the supply price of the units in their present use would not be equal, and this inequality gives rise to less than per­fect elasticity of supply of the input in its present use.

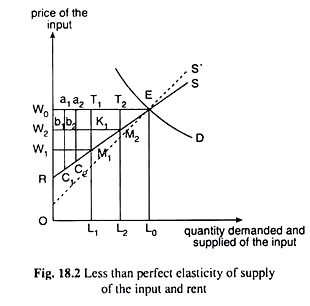
For, as the price of the input in its present use rises, its units with higher and higher supply price would transfer themselves from their alternative uses, i.e., as the price rises, the supply of the input in its present use also rises giving us an upward sloping supply curve of the input like the curve, S, in Fig. 18.2 along which the elasticity of supply is less than perfect (0 < e < ∞).

When the supply curve of the input is up­ward sloping, we have to remember the fol­lowing three points:

(i) The supply of the input would increase if its price increases. For exam­ple, at the price of W₁, the supply is L₁ and, as price increases to W₂, supply also rises to L₂.

(ii) The amount of rent earned by different units of the input would be different.

For example, when price is W₂, rent earned by the marginal unit (L₂th unit) of the input supplied is: price received-minimum supply price of the unit = W₂ – L₂M₂ = 0; but the rent received by an earlier unit, say, L₁th unit, is K₁M₁. Similarly, the rent received by two still earlier units are b₂C₂ and b₁C₁.

We may note, and it is seen from the Fig. 18.2, that at any price, say, W₂, the marginal (here L₂th) unit of the input supplied earns a zero rent, and the earlier units earn positive rent. Also, the earlier the unit, the larger is the amount of rent, because the earlier the unit, the smaller is the supply price.

Therefore, at any price, different units supplied of an input earn different amounts of rent. Further, at any price, say, W₂, if we add up the rents earned by all the indi­vidual units of the input (like b₁C₁, b₂C₂, etc.), the total amount of rent earned by the input would be equal to □W₂M₂R.

(iii) As the price of the input rises and more of it is supplied, the rent earned by the units already supplied would increase and the aggregate amount of rent earned by the input also rises. For example, if the price of the input rises from W₂ to W₀, its supply would increase from L₂ to L₀. As a result of the rise in price, rent of the units already supplied (up to L₂) would be larger.

For example, the L₂th unit previously earned a zero rent; now its rent would be T₂M₂. Also, the units that earned rent of the amounts b₁C₁ and b₂C₂ would earn now the amounts a₁Q₁ and a₂C₂, which are larger than the previous amounts.

It may be noted also that at the price of W₀, the rent earned by the marginal (L₀th) unit is zero and the aggregate amount of rent of the input is □W₀ER which as larger than □W₂M₂R at the price of W₂.

Therefore, that if the elasticity of supply of an input is less than perfect, then at any particular price of the input, its different units supplied would get different amounts of rent, the rent of the marginal unit supplied being zero.

We have also seen how the aggregate amount of rent of the input at any particular price is obtained as a geometrical area. Lastly, we have obtained that the aggregate amount of rent and rent of the individual units of the input would depend upon its price—the higher the price, the higher would be the aggregate amount of rent and rent of the individual units.

In Fig. 18.2, the supply and demand curves for the input have been given to be the curves S and D, respectively. The market equilibrium point is the intersection point E of these two curves and, at this point, we have obtained the price of the input to be W₀ and the equilibrium quantity demanded and supplied to be L₀.

At the price of W₀, we have already seen that the aggregate amount of rent is equal to □W₀ER. We have also seen how this amount may be obtained by aggregating the amounts of rent of the individual units.

However, the aggregate amount may also be obtained as the differ­ence between the aggregate amount of money received by the different units as their price represented by □OW₀EL₀ and the aggregate of their individual supply prices represented by □OREL₀, i.e., we have

Aggregate amount of rent of the input = □OW₀EL₀ – □OREL₀

= OW₀ER

We have seen that if the supply of an input is less than perfectly elastic, then it would be able to earn economic rent. We have also seen that at any particular price of the input, all its units barring the marginal unit, will earn a positive rent. However, it is very important to remember that rent of an input will be a fraction only of the price it receives.

For example, at the price of W₀, the L₂th unit of the input gets a rent of T₂M₂ which is only a part of the price, W₀ = T₂L₂, that it receives. Since the individual units (barring the marginal one) gets a rent which is less than the income (the price) it receives, the aggregate amount of rent of the input in this case would also be a fraction of aggregate income it receives.

For example, at the price of W₂, the aggregate income received by the input is □OW₂M₂L₂ and the aggregate amount of rent that the input earns is DW₂M₂R, which is only a part or fraction of aggregate income.

Infinite or Perfect Elasticity of Supply and Rent:

If the units of an input are equally efficient in their present use as also in their alternative uses, then all of them would receive the same amount of money in their next best alternative use, and, therefore, all the units would have the same supply price in their present use.

Under the circumstances, at the price equal to their minimum supply price, the supply of the input is infinitely large, because all the units of the input are willing to supply their services at this price.

Therefore, it is a case of perfectly elastic supply (e = ∞) of the input. On the other hand, if they are offered a price which is less than their minimum supply price, then no unit of the input would be willing to supply their service in the present use; in that case, the supply of the input would be equal to zero.

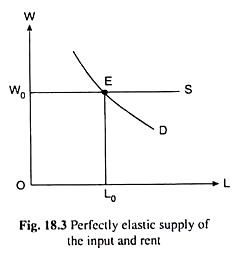
It follows, then, that if the supply of an input is perfectly elastic (e = ∞) its supply curve would be a horizontal straight line at the level of its minimum supply price, like the line S in Fig. 18.3.

If the supply of an input is perfectly elastic (e = ∞) the input would not have any rental surplus. For, as we have seen above, each unit of the input in this case, would receive a price equal to its supply price, i.e., it would receive no surplus or rent over and above its supply price.

Therefore, the aggregate amount of rent obtained by the input in this case is also zero. We may explain all this with the help of Fig. 18.3.

In Fig. 18.3, the minimum supply price of all the units of the input has been assumed to be W₀. Therefore, the supply curve of labour will be a horizontal straight line, S, at the level of W₀. The demand curve for the input is given by the curve D. At the equilibrium point E, the price of the input is W₀ and the quantity demanded and sup­plied is L₀.

It is obtained from Fig. 18.3 that the total amount of money received by L₀ units of the input is □OW₀EL₀ and the aggregate of supply prices, i.e., the minimum amount required by them, is also □OW₀EL₀. Therefore, economic rent of the input in this case would be □OW₀EL₀ – □OW₀EL₀ = 0. That is, if the supply of an input is perfectly elastic, the input would not enjoy any rent.

Share of Economic Rent in an Input’s Income:

In our discussion of the modern theory of rent, we have seen that economic rent enjoyed by an input depends upon the elasticity of its supply. We have seen that if this elasticity (e) = 0, then all the income received by the units of the input taken together is economic rent. Also, all the money received by each individual unit of the input as its price is economic rent.

At the other end, when e = the input in aggregate and also any of its individual unit do not enjoy any economic rent, i.e., not even a fraction of its income can be called the rental surplus. In between these two ends, when 0 < e < ∞, a portion—not all—of the income received in aggregate by all the employed units of the input is economic rent.

Similarly, a part of the price received by each individual unit of the input is a rental surplus over its supply price. Now, 0 < e < ∞, is a vast range. In this range, as e increases from zero to infinity, the fraction of income of the input which would be rent would fall from 100 per cent to zero per cent.

The modern theory of rent contends that not only land, but any other input can obtain rent if its supply is less than perfectly elastic. Since, as a gift of nature, the supply of land is more inelastic than any other input, Marshall (1842-1924) has said that rent of land is the leading species of a large genus.

Definition of an Input and Length of the Time Horizon, and Economic Rent:

The share of economic rent in an input’s income depends upon the elasticity of supply of the input. However, the elasticity of supply of an input depends, ceteris paribus, on (a) the manner in which we define an input and the uses to which it might be put and (b) time. If we adopt broad definitions of an input and its use, elasticity of its supply will be smaller and economic rent will be greater, and vice versa.

For example, if we group all the natural, non-human agents of production together and call them ‘land’, and if we define agriculture as the sole use of land, then the supply of land to agriculture will be perfectly inelastic.

On these definitions, land is quite specific to agriculture so that its supply price is zero. The whole of the actual earnings of the landowners will, therefore, be economic rent. However, economic rent will be smaller, the narrower are our definitions of use.

For example, if we distinguish between the use of land for growing corn, wheat, potatoes, apples, and so on, the supply price of land to each of these uses will be positive, so that only a part of its actual earnings in any particular use may be called economic rent.

If we go further and define as a separate use the growing of potatoes for Mr. X, who is one of the many growers of potatoes in a locality, then the market for the use of land for growing potatoes would be perfectly competi­tive. In this case, at the equilibrium market price for the use of land, the supply of land to any potato-grower would be perfectly elastic. And so, the amount of economic rent in this case would be zero.

Again, on any set of definitions of an input and its use, the supply price of a unit of the input to any use will depend on the range of alternative uses that is open to its owner, and this tends to vary directly with time.

If we define the short run as a period within which a unit of an input cannot move from one use to another, then its minimum supply price to its present use will be zero, and the whole of its current earnings will be economic rent.

But, in the long run, units of an input may move from one use to another, e.g., the carpenters may become bricklayers. In the long run, therefore, the supply price of each unit of an input to its existing use will be what it could earn in its next most remunerative use, and not the whole of its actual earnings will be economic rent.

It would seem then that wide definitions of inputs and their uses have the same effect on the size of economic rent as a narrow planning horizon, and that narrow definitions have similar consequences to a lengthening of planning horizon.

On the basis of the above analysis, we may conclude that the amount of economic rent depends upon the breadth of definition of a productive service and on the length of the planning horizon.