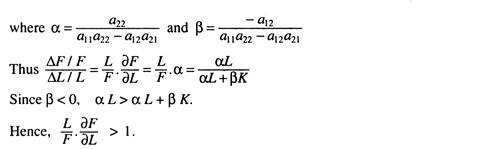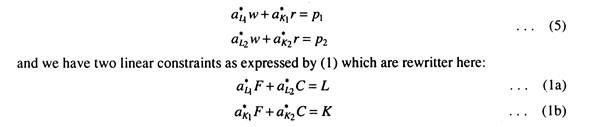The Rybczynski Theorem (RT) (With Diagram) | Economics

The Rybczynski Theorem (RT) says that if the endowment of some resource increases, the industry that uses that resource most intensively will increase its output while the other indus­try will decrease its output. The relative factor intensity is measured by the ratio of factor use in each industry.

The theorem suggests that unbalanced growth in factor supplies tends, at con­stant commodity prices, to lead to strong asymmetric changes in output level of two types of industries-capital-intensive and labour-intensive.

If the member of factors and commodities are evenly matched and two commodities (such as food and cloth) are not jointly produced, this asymmetry entails that growth in one factor, such as labour, acts as a force to cause an actual fall in the production of one commodity.

Let us suppose that cloth is capital-intensive and food is labour-intensive. Now if capital stock grows, the output of cloth will increase. However, the production of more cloth will lead to an increase in the demand for labour.

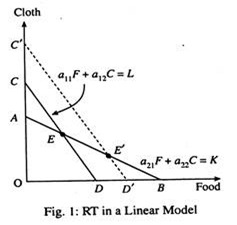
If more labour is not used with capital, the produc­tivity of labour is bound to fall. As a result, there will be shortage of labour in the labour-intensive sector (food). And the end result is a fall in the output of food. Thus capital accumulation will lead to a fall in output of the labour-intensive industry. The RT can be presented in two types of models – a linear model and a non-linear model. In Fig. 1, we show the RT in a linear model.

Here we have the following two linear constraints:                      

a₁₁F + a₁₂C = L (Labour) (1a)

a ₂₁ F + a₂₂C = K (Capital) (1b)

where a₁₁, a₁₂-etc., are input coefficients of the Leontief type. Optimum production of the two goods and the maximum income occur at point E. The slope of the labour constraint is and the slope of the capital constraint is – a₂₁/a₂₂

This means that, industry 1, food, is labour-intensive and industry 2, cloth, is capital-intensive.

If the amount of labour is increased, the labour constraint shifts to the right, and a new output mix is produced at point E’. At E’, output of food, the labour-intensive good, is in­creased, while the output of the capital-intensive good (cloth) falls.

Thus, the RT simply suggests that if product prices are held constant, an increase in the supply of one factor, say labour will lead to an increase in output of the labour-intensive good and a fall in output of the capital-intensive good.

Algebraic Proof:

The RT can also be proved by using a system of simultaneous equations.

In this case, the solution values of the model are determined by capital and labour constraints:

These are Rybczynski results. Moreover, with any change in some factor endowment, the output that is intensive in that factor will change in greater absolute proportion than the param­eter change. For example F = αL + βK.

An identical result follows for the change in C with respect to a change in capital. The output levels of each industry responds elastically to change in factor endowments in which they are intensive.

The RT in Non-Linear Models:

The RT can be interpreted as the comparative statics of the two-factor variable proportion model with respect to changes in endowments. One basic hypothesis of Samuelson s factor price equalisation theorem which includes the assumption that one industry is always more labour-intensive than the other is that a change in the factor endowment of either labour or capital (or both) will have no effect on factor prices.

According to factor price equalisation then, factor prices are functions of output prices only. This follows from the fact that input coefficients are functions of the factor price ratio a_tj = a*(w/r) and w = w* (p₁ p₂).

Thus the first important result is that

Here we hold output prices constant and change only the factor endowments. We may now consider the effects of changing the endowment of capital, say, on output levels. Since the price of each commodity is equal to unit cost under competitive conditions we have

Here we have assumed linear homogeneity of the production function to express the < s as function of the factor price ratio (w/r) only. If now either labour or capital changes, the a_ij s remain constant, since [∂_aij/∂ (w/r)]. [∂ (w/r)/dL]=0 and since the [(∂w/r)/∂L] = 0 from (2).

Let us now differentiate equations (1) partially w. r. t. labour (we drop the asterisks for sim­plicity).

These results-known as Rybczynski theorem’ states that an increase, say, in the endowment of labour (holding output prices constant) will increase the output of the labour-intensive (food) industry and decrease that of the capital-intensive (cloth) industry.

The converse is also true. An increase in the endowment of capital, ceteris paribus, will increase the output of the capital-intensive cloth industry and decrease that of the labour-intensive food industry However all these repercussions will leave factor prices unchanged.

Duality of the Two Theorems:

There is a reciprocity relationship between the SST and RT. This states that in. any general equilibrium model, the effect of an increase in commodity price (say _P1) on the return to a factor (say _Wi) _s the same as the effect of an increase in the corresponding factor endowment (v_i) on the output of commodity. However, in each case, some other set of variables are held constant. Thus

with all other commodity prices and all factor endowments held constant in the left hand de­rivative and all other endowments and all commodity prices held constant in the right hand derivative. This relationship reveals the dual nature of SST and RT theorems.

If an increase in the price of cloth lowers agricultural wages, then an increase in the endowment of rural labours a constant wage) would lower the output of cloth. In each case it is the presumed capital- intensity of cloth which is operative.

In the 2 x 2 case, both the SST and RT, thus, reflect the magnification effects that stem directly from the assumed lack of joint production. Putting a hat (a) over a variable to indicate relative changes, if cloth is capital-intensive and food is labour-intensive and if the relative price of cloth rises then

In addition, if the economy grows, but with capital (capital) growing at a faster rate than labour

Inequality (7) shows that commodity price changes are trapped between factor price changes (since both the factors are required to produce each good), while inequality (8) shows that in order to absorb endowment changes the composition of outputs (each of which uses both the factors) must change more drastically. SST stressed the first inequality in (7) while RT focused on the last inequality in (8), assuming L equals zero.