Theory of Games: Definition and Digression

The interdependence of firms in oligopolistic markets and the inherent uncertainty about competitors’ reactions to any course of action adopted by a firm cannot be analysed effectively by the traditional tools of economic theory.

Economists have developed collusive models, limit-pricing models, managerial models, and behavioural models, but these do not provide a general theory of oligopoly in the sense that none of these models could fully explain the decision-making process of oligopolists.

A different approach to the study of the oligopoly problem is provided by the theory of games. The first systematic attempt in this field is von Neumann’s and Morgen stern’s Theory of Games and Economic Behaviour, published in 1944. Since that time numerous economists have developed models of oligopolistic behaviour based on the theory of games. Perhaps the most prominent proponent of the games-theory approach is Martin Shubik, who seems to believe that the only hope for the development of a general theory of oligopoly is the games theory.

Despite such enthusiasts the games- theory approach has not yet provided results which could lead to a general theory of oligopoly. The main contribution of this approach is that it can use high-speed computers to conduct experiments of oligopolistic behaviour. Such controlled experiments cannot be conducted in the real business world. Thus the computerized study of oligo­polistic behaviour is an extremely useful tool which might lead to generalizations about the decision-making process of oligopolists in real world situations, and thus provide the basis for a theory of oligopoly. This development, however, is still in its infancy, and has not as yet gained much acclaim by the majority of economists.

Some Definitions:

The firm has various instruments or policy variables with which it can pursue its goals. The most important are the price, quantity and style of its products, advertising and other selling activities, research and development expenditures, channels for selling the product(s), and changes in the number of products (discontinuation of an old product or introduction of new ones).

A strategy is a specific course of action with clearly defined values for the policy variables. For example, a strategy may consist of setting a price of £3-95, spending £2000 on advertising, making a change in the packaging of the product, and selling it in supermarkets. Another strategy may involve leaving the price unchanged, spending £1000 on advertising, devoting £2000 to research on a new product, and so on.

To each of these strategies a competitor may react in different ways, that is, by adopting different strategies. He may decide to adopt the same or a different course of action than the one adopted by the other firm. Thus each firm has various strategies open to it, and in any particular case it will adopt the one that will seem most advantageous under the circumstances.

The payoff of a strategy is the ‘net gain’ it will bring to the firm for any given counter- strategy of the competitors). This gain is measured in terms of the goal(s) of the firm. For example, if the goal of the firm is to maximise its profit, the payoffs of a strategy will be measured in terms of profit levels that it yields; if the goal is maximisation of the market share, the payoffs will be measured as the actual shares that the strategy will secure to the firm adopting it.

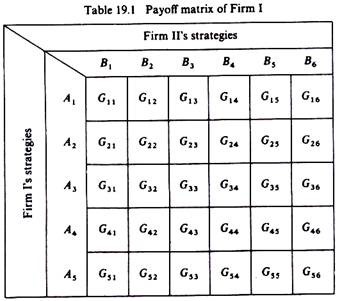
The payoff matrix of a firm is a table showing the payoffs accruing to this firm as a result of each possible combination of strategies adopted by it and by its rival(s). For example, assume that there are two firms in the industry. Firm I has to choose among five strategies (A₁, A₂, …, A₅) and Firm II can react by adopting any one of six strategies open to it(B₁, B₂,…, B₆).

Thus to each strategy of Firm I there are six possible counter- strategies of Firm II, and similarly to each strategy of Firm II there are five counter- strategies of the rival Firm I. Thus the payoff matrix of each firm will include 5 x 6 = 30 payoffs, corresponding to the results of each possible combination of strategies selected by both rivals.

Let us denote each payoff G_ij, where i refers to the strategy adopted by Firm I and j to the counter-strategy adopted by Firm II. Thus for the above example the payoff matrix for Firm I will be of the general form of table 19.1. If Firm I adopts strategy A, and its rival reacts by adopting among the strategies open to it B₅, the payoff (gain) of Firm I will be G₁₅. If Firm I chooses strategy A₄ and its rival reacts with strategy B₆, the payoff of Firm I will be g₄₆, and so on.

In the theory of games the firms in oligopolistic markets are treated as players in a chess game to each movement by one player the other may choose among several counter-movements. The counter-movements of rivals are probable but not certain. Yet it is possible to choose a strategy which (under certain conditions) will maximise the firm’s expected ‘gain’, after making due allowance for the effects of rivals’ probable reactions.

The Prisoner’s Dilemma: A Digression:

We saw that in most cases of variable-sum games the maximin-minimax behaviour leads the rivals to suboptimal solutions, that is, to situations worse than they need be. These examples and their suboptimal solutions are a special case of the general group of problems which are known as Prisoner’s Dilemma Games. A brief exposition of the original prisoner’s dilemma might help the understanding of the behaviour of firms faced by uncertainty about their rivals’ action.

Two criminals are arrested after committing a big bank robbery. However, the evi­dence is not adequate to make the robbery charge stand unless one or both criminals confess. Each suspect is interrogated in isolation from his companion so that no com­munication is possible between them.

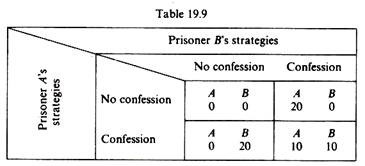
The District Attorney promises no punishment for the suspect who confesses and a heavy sentence of, say, twenty years’ imprisonment for the other party. If both suspects do not confess, both will go free. If both confess, they will get the sentence prescribed by the law for the crime of robbery, for example ten years’ imprisonment.

Thus each suspect has two ‘strategies’ open to himself, to confess or not to confess, and is faced with the dilemma to confess (and go free if the other does not confess, or get the ten-year sentence) or not to confess (and go free if the other does not confess, or get the heavy twenty-year sentence if he is betrayed by the other suspect). The payoff matrix of the two prisoners is shown in table 19.9.

Given the lack of communication between the suspects and the uncertainty as to the ‘loyalty’ of the other prisoner, each one of them prefers to adopt the second strategy, that is, to confess, so that both get a ten-year sentence. Clearly this is a worse situation as compared with the adoption of the ‘no confession’ strategy by both robbers.

The ‘dominant’ strategy, which implies the rule ‘expect the worst from the other (s)’ (the maximin assumption) leads to a worse position than the robbers need be in! If communication were possible, or if from past experience the fellows had learned to trust each other, they would both plead ‘not guilty’ and would go free, thus maximising their ‘gains’ The drawing of analogies concerning the conditions of uncertainty facing the firms in oligopolistic markets is straightforward.