We will illustrate this model with a duopolistic market in which the firms aim at the maximisation of their profit.
Their products are close substitutes so that if their prices differ the firm with the lower price will supply the largest part of the market.
It is assumed that the firms will use price as their instrumental variable. For simplicity we assume that each firm can charge two prices (either £3 or £5), that is, there are two strategies open to each competitor.
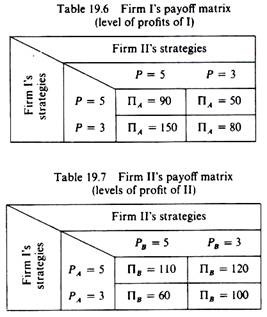
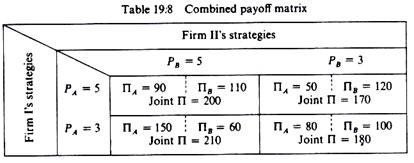
Each firm has a different cost structure and the market size is affected by the rivals’ combined action. Under these conditions the payoff matrix of each firm is expressed in terms of levels of profit, and the gains of one rival need not be (and in our example are not) equal to the losses of the other. The payoff matrices of the two firms are shown below in tables 19.6 and 19.7, and are subsequently combined in a single table. (Table 19.8.)
The behavioural rule is the same for both firms each expects the worst from the rival. The choice of Firm I is a maximin strategy. If Firm I sets the price of £5 the minimum gain is £50; if it sets p = 3 its minimum profit is £80. Among these two minima the firm chooses the maximum, that is, the preferred strategy by Firm I is p = 3. The choice of Firm II is also a maximin strategy. If Firm II charges a price of £5 the worst it can expect is a profit of £60; if it charges a price of £3 the minimum level of profit is £100. Among these minima the firm will choose the maximum, that is, Firm II will choose the price of £3.
Under these circumstances there is a unique equilibrium price (£3) which will be adopted by both firms. Thus the strategy F = £3 is a dominant strategy. Yet with this strategy both firms are in a worse situation as compared to the alternative strategy p = 5, since both realise a lower profit. And of course the industry (joint) profit is not maximised.
The conservative maximin strategy is not the optimal solution in this case. If the firms colluded and both charged the higher price of £5 the joint profit and their individual profits would be higher (90 > 80,110 > 100, and 200 > 180). Thus while the maximin strategy provides an optimal solution in the zero-sum game, this may not be so in the variable-sum game.
ADVERTISEMENTS:
Many other oligopolistic actions may be analysed with the above apparatus of the theory of games. For example, advertising campaigns, change in style or diversification, research and development expenditures may be examined by the principles of the games theory. In most real-world cases we see that firms choose strategies which do not maximise their profits: advertising or new-product rivalry often lead to excessive increases in costs of all firms in the industry. Such situations may be explained by the conservative behaviour of maximin strategies.
In many oligopolistic situations firms seem to avoid the unfavourable outcomes predicted by the maximin-minimax behaviour of the theory of games. Several reasons have been offered for these cases.
Firstly, the duration of rivalry. If rivalry has been continuous for a considerable time-period the rivals ‘learn’ to predict the reactions of each other and this leads to the avoidance of moves which, from well-established past patterns, have proved disadvantageous to all parties.
Secondly, the stability of tastes and processes. Firms are more likely to avoid mutually damaging actions in a market where demand does not change and technological progress is slow. On the other hand, in markets with frequent changes of tastes it is almost certain that firms will adopt maximin strategies despite their mutually unfavourable results. Thirdly, the existence of common sources of information and communication between rivals. If the rivals lack information it is most natural to fear the worst (maximin assumption) from the competitors and reach suboptimal solutions.
ADVERTISEMENTS:
Fourthly, time-lags are important in deciding which strategy to adopt. If the imitation of an action (for example, a new product, a new process) is easy the firms will recognize that they have little to gain and much to lose by aggressive action and hence will adopt maximin strategies, which are by their nature conservative. If, however, an action cannot easily or quickly be imitated the firms will tend to abandon maximin attitudes and adopt actions which lead to more favourable positions for themselves, instead of expecting the worst from their rivals, for the simple reason that the rivals cannot quickly adopt the most advantageous action.
In summary games theory has not provided a general theory of oligopolistic behaviour. However, the games-theory approach has been able to explain some real-world situations. It has helped in showing that there are strong incentives for collusion in several oligopolistic situations. Perhaps the most important contribution of this theory is that it has led to controlled experiments in the study of firms’ behaviour. By expressing the alternatives open to a firm and its rivals in the form of payoff matrices it has made possible the examination of an increasing number of alternatives with controlled experiments based on the use of high-speed computers.
Playing ‘monopoly games’ with computers has been a fashionable tendency in many American universities. Such ‘controlled’ studies have provided insight into various aspects of the decision-making process of individuals in uncertain situations similar to those facing the firms in the real world. Yet games theory is still a long way from providing a comprehensive theory of oligopolistic behaviour.