Pigou’s Ideal Output: Concept, Assumptions and Explanation

Pigou’s Ideal Output: Concept, Assumptions and Explanation!

Pigou’s concept of ideal output is related to the optimum welfare of the economic system. Pigou uses the size of the national dividend as an indicator of welfare. According to Pigou, national dividend is maximised when the value of the marginal social product of all resources is equal in all possible uses. Under perfect competition, this optimum or ideal output is reached automatically.

If, however, the value of the social marginal product of resources is less in any one use than in any other, the ideal output is attained by transferring resources to more fruitful modes of production by social control or by a tax or bounty.

Prof. Baumol has reinterpreted Pigou’s concept of ideal output and has related it to the Paretian overall equilibrium. He defines the ideal output as that output at which no reallocation of the economy’s resources among various uses would make the society better-off than before. This definition of ideal output is similar to Paretian position which states that welfare is maximised if at least one person is made better-off with no change in the position of others by any economic reorganization. Baumol discusses the problem of ideal output in terms of the modern analytical tools of welfare economics.

Assumptions:

His analysis is based on the following assumptions:

(1) There is perfect competition on the demand side of the market for finished goods.

(2) All goods are uniquely distributed in society.

(3) Tastes and technology remain unchanged in society.

(4) Every member of the society prefers more rather than less of each good.

(5) There is a given level of employment of resources.

(6) There are no external effects in consumption and production.

(7) Community indifference curves do not intersect each other.

(8) The economy produces only two goods, say X and Y.

Explanation:

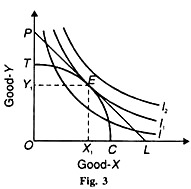
Given these assumptions, Baumol demonstrates diagrammatically how society reaches the ideal output position. Consider Figure 3 where the output of good X is measured along the horizontal axis and of good Y along the vertical axis. I, I₁, and I₂ are the community indifference curves showing various possible combinations of these goods available to the society. The slope of an indifference curve at any point shows the marginal о rate of substitution (MRS) between the two goods X and Y (MRS_xy).

TC is the transformation curve showing various output combinations possible with the given resources and technology. The slope of the transformation curve at any point measures the ratio of the marginal social cost (MSC) of X to that of Y. The slope of the transformation curve is the marginal rate of transformation (MRT) between two goods X and Y in our case. Thus MRT = MSC_x/MSC_y . PL is the price line whose slope shows P_x /Р_y.

The society attains the ideal output position E where the transfor­mation curve TC touches the highest possible community indifference curve TC produces and consumes OX₁ of good X and OY₁ of good Y. Any movement along the TC curve away from point E brings the community to a lower indifference curve, such as the curve I and to a lower level of welfare.

It can be shown that this ideal output is, in fact, the competitive output. Since it is assumed that there is perfect competition and absence of external effects, prices of the two goods remain uniform throughout the market. Thus, from the demand side, equilibrium is established at point E where the price line PL is tangent to the indifference curve I₁, Thus at point E, MRS_xy = P_x/P_y……… (1).

From the supply side, the competitive equilibrium requires that the slope of the price line must equal the slope of the transformation curve, P_x/P_y = MRT_xy…. (2)

In fact, MRT_xy is equal to the ratio of the marginal private cost of X (MC_x ) to that of Y (MC_y) in a perfect market. Since it is assumed that the external effects in production are absent, therefore, the marginal private cost equals the marginal social cost of production. Thus the slope of the transformation curve shows MRTxy = MC_x/МС_y = MSC_x/MSC_y.

It fellows from (1) and (2) that competitive output is determined where the transformation curve, the price line and the indifference curve are tangent to each other, MRT_xy = P_x/P_y = MRS_xy. This is the point E in Figure 3.

In fact, this competitive equilibrium is Paretian overall equilibrium or Paretian optimality. But the ideal output is determined where the transformation curve is tangent to the indifference curve. It is only in the absence of external effects that the competitive output (or Paretian optimality) position is the same as the ideal output, shown as E in Figure 3.

If, however, external effects are present in the industry producing good X, The marginal social cost in it will diverge from its marginal private cost. Thus the ratio between the marginal social cost in this industry and that in other industry producing good Y will not equal the ratio between their prices. In other words, the transformation curve and the price line will not be tangent to each other.

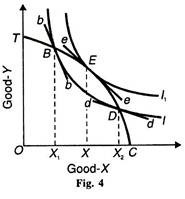
First, consider the case when the product of good X involves external economies. The price line required for equilibrium in production is shown by the line bb in Figure 4. The slope of this line is greater than that of the transformation curve TC which implies that the marginal private cost is greater than the marginal social cost. Now consider that the production of good X involves external diseconomies. The price line is shown by dd whose slope is smaller than that of the transformation curve TC. Here the marginal social cost is greater than the marginal private cost.

In the absence of external effects, E is the point of ideal output where the indifference curves I₁, and the transformation curve TC is tangent to each. This is also the position of competitive output because the price line ее, the indifference curve I₁, and the transformation curve TC are tangent to each other. If good X is produced under conditions of external economies of production, the point of equilibrium will be at В to the left of E.

Here the price line bb is tangent to the indifference curve I at point В where the output OX₁ of good X is very small as compared to the ideal output OX. If good X is produced under conditions of external diseconomies, the point of equilibrium will be D to the right of E. Here the price line dd is tangent to the indifference curve I at point D where the output OX₂ of good X is very large as compared to the ideal output OX. Points В and D cannot be of ideal output because they lie on a lower indifference curve I while point E is on a higher indifference curve I₁.

Like Pigou, Baumol suggests that the external effects can be corrected and ideal output obtained by a system of taxes and bounties. If the production of good X is in excess of the ideal output as at point D, it can be reduced by imposing a heavy tax on each unit of output. On the contrary, if the output of X is less than the ideal output as at point B, output can be increased by a large bounty per unit of output. The position of ideal output can be attained if the amount collected by tax equals the amount paid by the government as bounty.